Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho \(x;y;z\ge0\)và \(xy+yz+zx=1\)Tìm GTLN
\(Q=9\left(x^2+y^2+z^2\right)-4\left(x^3+y^3+z^3\right)\)


Ta có: \(\left(x+z\right)\left(y+z\right)=1\)
\(\Rightarrow\left(x+z\right)^2\left(y+z\right)^2=1\)
\(\Rightarrow P=\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{\left(y+z\right)^2}+\dfrac{1}{\left(z+x\right)^2}=\dfrac{1}{\left(x-y\right)^2}+\dfrac{\left(x+z\right)^2\left(y+z\right)^2}{\left(y+z\right)^2}+\dfrac{\left(x+z\right)^2\left(y+z\right)^2}{\left(z+x\right)^2}\)
\(\Rightarrow P=\dfrac{1}{\left(x-y\right)^2}+\left(x+z\right)^2+\left(y+z\right)^2\)
\(\Rightarrow P=\dfrac{1}{\left(x-y\right)^2}+\left(x+z\right)^2-2\left(x+z\right)\left(y+z\right)+\left(y+z\right)^2+2\) (Vì: (x+z)(y+z)=1 =>2(x+z)(y+z)=2 )
\(\Rightarrow P=\dfrac{1}{\left(x-y\right)^2}+\left(x+z-y-z\right)^2+2\)
\(\Rightarrow P=\dfrac{1}{\left(x-y\right)^2}+\left(x-y\right)^2+2\)
Áp dụng bất đẳng thức Cauchy, ta có :
\(\dfrac{1}{\left(x-y\right)^2}+\left(x-y\right)^2\ge2\sqrt{\dfrac{1}{\left(x-y\right)^2}\cdot\left(x-y\right)^2}=2\cdot1=2\)
\(\Rightarrow P=\dfrac{1}{\left(x-y\right)^2}+\left(x-y\right)^2+2\ge2+2=4\)
Vậy \(MinP=4\) khi \(x-y=1\); \(y+z=\dfrac{\sqrt{5}-1}{2}\); \(x+z=\dfrac{2}{\sqrt{5}-1}\)

a )
Sử dụng Cô-si , ta có :
\(x+y\ge2\sqrt{xy}\) (1)
\(\dfrac{1}{x}+\dfrac{1}{y}\ge2\sqrt{\dfrac{1}{x}.\dfrac{1}{y}}\) (2)
Nhân cả vế (1) vế (2) lại ta có :
\(\left(x+y\right)\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\ge2\sqrt{xy}.2\sqrt{\dfrac{1}{x}.\dfrac{1}{y}}=4\)
\(\LeftrightarrowĐPCM.\)

Bài 2 bạn tham khảo cách làm của cô Linh Chi tại đây nhé :
Câu hỏi của nguyen trung nghia - Toán lớp 8 - Học toán với OnlineMath
Học tốt và cá tháng tư đừng để bị troll nha !!!!!!!!!!!
B1:
\(M=\left(x+y\right)\left(\frac{1}{x}+\frac{1}{y}\right)\)
\(=2+\frac{x}{y}+\frac{y}{x}\)
Nhờ dự đoán được điểm rơi,ta chứng minh bất đẳng thức sau luôn đúng:\(\frac{x}{y}+\frac{y}{x}\le\frac{5}{2}\)
Thật vậy !!!
\(\frac{x}{y}+\frac{y}{x}\le\frac{5}{2}\)
\(\Leftrightarrow\left(\frac{x}{y}-\frac{1}{2}\right)+\left(\frac{y}{x}-2\right)\le0\)
\(\Leftrightarrow\frac{2x-y}{2y}+\frac{y-2x}{x}\le0\)
\(\Leftrightarrow\frac{2x^2-xy+2y^2-4xy}{2xy}\le0\)
\(\Leftrightarrow2x^2-5xy+2y^2\le0\)
\(\Leftrightarrow\left(x-2y\right)\left(2x-y\right)\le0\) ( đúng )
Dấu "=" xảy ra tại \(x=1;y=2\)
Vậy \(M_{max}=\frac{9}{2}\Leftrightarrow x=1;y=2\)

a: x-y-z=0
=>x=y+z; y=x-z; z=x-y
\(K=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}=\dfrac{y\cdot\left(-z\right)\cdot x}{xyz}=-1\)
b: Tham khảo:
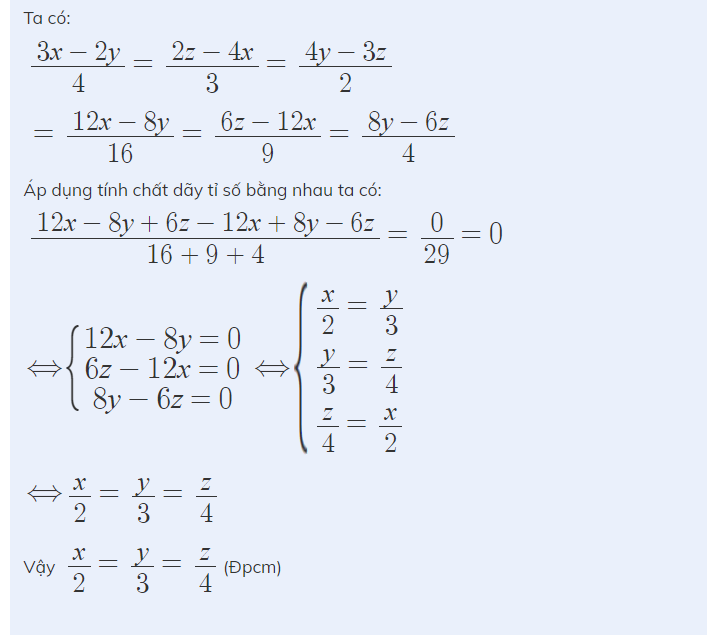

a) A=(x+z)(y+t)
= xy+xt+zy+zt
Áp dụng bất đẳng thức cô si cho 2 số ta có
x2+y2 ≥ 2\(\sqrt{x^2y^2}\)
⇔x2+y2 ≥ 2xy
TT ta có
x2+t2 ≥ 2xt
y2+z2 ≥ 2yz
z2+t2 ≥ 2zt
cộng vế vs vế ta có
=> x2+y2+x2+t2+y2+z2+t2 ≥ 2xy+2xt+2yz+2zt
⇔ 2(x2+y2+z2+t2) ≥ 2(xy+xt+yz+zt)
⇔ 2 .1 ≥2 A
⇔ 1≥ A
⇔ A ≤ 1
=> Max A =1 dấu "=" xảy ra khi x=y=t=z= \(\pm\dfrac{1}{2}\)
Câu b)
Đây là bài toán quen thuộc của dạng toán xác định điểm rơi trong BĐT Cô-si:
Áp dụng BĐT Cô-si:
\(\frac{2}{3}x^2+\frac{2}{3}y^2\geq 2\sqrt{\frac{2}{3}x^2.\frac{2}{3}y^2}=\frac{4}{3}|xy|\geq \frac{4}{3}xy\)
\(\frac{1}{3}x^2+\frac{4}{3}t^2\geq 2\sqrt{\frac{1}{3}x^2.\frac{4}{3}t^2}=\frac{4}{3}|xt|\geq \frac{4}{3}xt\)
\(\frac{1}{3}y^2+\frac{4}{3}z^2\geq 2\sqrt{\frac{1}{3}y^2.\frac{4}{3}z^2}=\frac{4}{3}|yz|\geq \frac{4}{3}yz\)
\(\frac{2}{3}z^2+\frac{2}{3}t^2\geq 2\sqrt{\frac{2}{3}z^2.\frac{2}{3}t^2}=\frac{4}{3}|zt|\geq \frac{4}{3}zt\)
Cộng theo vế các BĐT thu được và rút gọn:
\(\Rightarrow x^2+y^2+2z^2+2t^2\geq \frac{4}{3}(xy+xt+yz+zt)\)
\(\Leftrightarrow \frac{4}{3}(xy+xt+yz+zt)\leq 1\)
\(\Leftrightarrow B=(x+z)(y+t)\leq \frac{3}{4}\) hay $B_{\max}=\frac{3}{4}$
Dấu bằng xảy ra khi \(x=y=2z=2t\Leftrightarrow (x,y,z,t)=\left(\frac{1}{\pm \sqrt{3}}; \frac{1}{\pm\sqrt{3}}; \frac{1}{\pm 2\sqrt{3}}; \frac{1}{\pm 2\sqrt{3}}\right)\)

a) Ta có: \(x=a^2-bc\Rightarrow ax=a^3-abc;\) \(y=b^2-ac\Rightarrow b^3-abc;\) \(z=c^2-ab\Rightarrow cz=c^3-abc\)
\(\Rightarrow ax+by+cz=a^3+b^3+c^3-3abc\)
Ta có: \(a^3+b^3+c^3-3abc=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2+2ab-ac-bc\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2-bc+b^2-ac+c^2-ab\right)=\left(a+b+c\right)\left(x+y+z\right)\)
Vậy: \(\left(x+y+z\right)\left(a+b+c\right)=ax+by+cz\left(đpcm\right)\)
#)Giải :
a) Ta có :
\(x=a^2-bc\Rightarrow ax=a^3-abc\)
\(y=b^2-ac\Rightarrow by=b^3-abc\)
\(z=c^2-ab\Rightarrow cz=c^3-abc\)
\(\Rightarrow ax+by+cz=a^3+b^3+c^3-3abc\)
Ta có : \(a^3+b^3+c^3-3abc=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2+2ab-ac-bc\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2-bc+b^2-ac+c^2-ab\right)=\left(a+b+c\right)\left(x+y+z\right)\)
\(\Rightarrow\left(x+y+z\right)\left(a+b+c\right)=ax+by+cz\left(đpcm\right)\)

Ta có: x+5y=21 và 2x+3z=51
=> x+5y+2x+3z=21+51
<=> 3x+3y+3z+2y=72
<=> 3(x+y+z)=72-2y
=> \(x+y+z=\frac{72-2y}{3}=24-\frac{2y}{3}\)
=> \(A=\left(x+y+z\right)^2=\left(24-\frac{2y}{3}\right)^2\)
Do \(y\ge0\)=> Để A đạt GTLN thì y đạt GTNN
Mà GTNN của y là y=0 => \(A_{max}=\left(24-\frac{2y}{3}\right)^2=\left(24-\frac{2}{3}.0\right)^2=24^2=576\)
Đáp số: Amax=576