Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

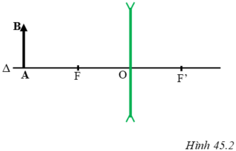
** Muốn dựng ảnh của một vật AB qua thấu kính phân kì khi AB vuông góc với trục chính, A nằm trên trục chính, ta làm như sau:
Dùng hai trong ba tia sáng đã học để dựng ảnh B’ của điểm B.
+ Tia BI đi song song với trục chính nên cho tia ló có đường kéo dài đi qua F
+ Tia tới BO là tia đi quang tâm O nên cho tia ló đi thẳng
+ Hai tia ló trên có đường kéo dài giao nhau tại B’, ta thu được ảnh ảo B’ của B qua thấu kính.
+ Từ B’ hạ vuông góc với trục của thấu kính, cắt trục chính tại điểm A’. A’ là ảnh của điểm A. A’B’ là ảnh ảo của AB tạo bởi thấu kính phân kỳ. (Hình 45.2a)
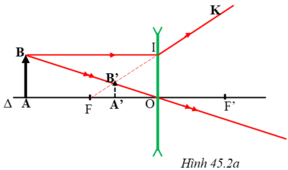
** Ta dựa vào tia đi song song trục chính và tia đi qua quang tâm để dựng ảnh A'B' của AB. Khi tịnh tiến AB luôn vuông góc với trục chính thì tại mọi vị trí, tia BI luôn không đổi, cho tia ló IK cũng không đổi. Do đó tia BO luôn cắt tia IK kéo dài tại B' nằm trong đoạn FI → Hình chiếu A’ của B’ lên trục chính nằm trong đoạn OF. Chính vì vậy, ảnh A'B' luôn nằm trong khoảng tiêu cự của thấu kính.

Đáp án: A
Ảnh S' là ảnh thật
Áp dụng công thức:
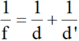
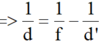
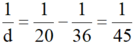
=> d = 45 cm
Vậy để thu được ảnh S' là ảnh thật và cách thấu kính 36cm thì khoảng cách từ vật đến thấu kính là 45cm

a) Vì trục chính của thấu kính phải vuông góc với màn và đi qua A, nên ta có thể xác định vị trí của thấu kính bằng cách vẽ tia sáng từ A tới thấu kính, sau đó vẽ đường thẳng vuông góc với màn và đi qua điểm giao của tia sáng và màn. Thấu kính sẽ nằm trên đường thẳng này, với tiêu điểm cách đường thẳng đó một khoảng bằng tiêu cự f của thấu kính.
Vì AB song song với màn M nên ảnh A' sẽ nằm trên cùng một đường với A, và A' cũng phải nằm trên đường thẳng vuông góc với màn và đi qua A. Để tìm tiêu cự của thấu kính, ta cần tìm vị trí của A' trên đường thẳng này.
Vì M và AB song song, nên tia sáng từ A tới thấu kính sẽ đi thẳng qua TKHT. Gọi F là tiêu điểm của TKHT, ta có thể vẽ tia sáng từ A tới F, sau đó vẽ tia phản chiếu đi qua F và đi tiếp qua thấu kính. Tại điểm mà tia này cắt đường thẳng vuông góc với màn và đi qua A, sẽ là vị trí của A'.
Ta cần tìm vị trí của F và tính khoảng cách từ F tới đường thẳng vuông góc với màn và đi qua A để tìm vị trí của A'. Gọi d là khoảng cách giữa M và TKHT, và gọi h là khoảng cách giữa A và M. Theo định luật phản xạ của ánh sáng, ta có: 1/d + 1/h = 1/f
Vì A' nằm trên đường thẳng vuông góc với màn và đi qua A, nên khoảng cách từ A' tới M sẽ bằng h, và khoảng cách từ A' tới TKHT sẽ bằng 2d (vì A' cách TKHT 2d). Do đó, ta có: 1/2d + 1/h = 1/f
Vì ta biết rằng chỉ có một vị trí của thấu kính cho ảnh rõ nét trên màn, nên A' phải nằm trên đường thẳng vuông góc với màn và đi qua A. Vì vậy, ta chỉ cần tìm giá trị của h mà trong đó có một vị trí của A' thỏa
Để ảnh A' rõ nét trên màn, thì tia sáng từ A tới thấu kính phải đi qua tiêu điểm F của TKHT. Vì vậy, vị trí của A' sẽ nằm trên đường thẳng vuông góc với màn và đi qua F. Để đảm bảo rằng chỉ có duy nhất một vị trí của A' thỏa điều kiện này, thì ta cần đảm bảo rằng tia sáng từ A tới F không cắt AB.
b) Giả sử AB nằm ngang, tức là vuông góc với trục chính của thấu kính. Ta cố định AB, sau đó dịch chuyển màn tới vị trí cách AB một khoảng x. Ta cần tìm giá trị của x sao cho có hai vị trí của thấu kính cho ảnh A' rõ nét trên màn, với tỉ lệ kích thước giữa A'1B'1 và A'2B'2 là 4:1.
Gọi y là khoảng cách giữa màn và trục chính của thấu kính. Ta sẽ tìm hai vị trí của thấu kính bằng cách tìm hai giá trị khác nhau của y.
Giả sử thấu kính nằm ở vị trí đầu tiên, với tiêu điểm F1 và khoảng cách y1. Khi đó, tia sáng từ A sẽ đi thẳng qua F1, sau đó đi qua thấu kính và tạo ảnh rõ nét A'1B'1 trên màn. Vì A'1B'1 có tỉ lệ 4:1 với AB, nên ta có thể tính được khoảng cách giữa F1 và màn bằng cách sử dụng tỉ lệ này. Gọi z là khoảng cách giữa F1 và màn, ta có: z + y1 = 5y
Tiếp theo, ta sẽ tìm vị trí của thấu kính thứ hai. Khi thấu kính được dịch chuyển đến vị trí này, tia sáng từ A sẽ đi thẳng qua tiêu điểm F2 của TKHT, sau đó đi qua thấu kính và tạo ảnh rõ nét A'2B'2 trên màn. Vì A'2B'2 có tỉ lệ 4:1 với AB, nên ta cũng có thể tính được khoảng cách giữa F2 và màn. Gọi y2 là khoảng cách giữa trục chính của thấu kính và màn ở vị trí này, ta có: y2 + z = 3y
Do đó, ta có hệ phương trình sau đây: y1 + z = 5y y2 + z = 3y
Giải hệ phương trình này, ta được: y1 = 2y y2 = -y
Vì y2 phải là khoảng cách dương, nên ta loại bỏ nghiệm này và chỉ giữ lại nghiệm y1 = 2y. Tức là, khoảng cách giữa trục chính của thấu kính và màn là 2 lần khoảng cách giữa AB và màn.
Khi đó, khoảng cách giữa màn và thấu kính tại vị trí này là: z + y1 = 5y - y1 = 3y
Do đó, ta có x = 32cm - (z + y1) = 32cm - 3y = 32cm - 6 * AB.
Vậy kết quả là x = 32cm - 6 * AB.