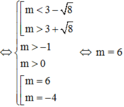Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm của (P) và (d) là \(x^2=mx-m+1\)\(\Leftrightarrow x^2-mx+m-1=0\)
Để (d) cắt (P) tại 2 điểm phân biệt thì \(\Delta=\left(-m\right)^2-4.1\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2>0\)\(\Leftrightarrow m-2\ne0\)\(\Leftrightarrow m\ne2\)
Khi đó \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=m-1\end{cases}}\)(hệ thức Vi-ét)
Độ dài cạnh huyền của tam giác vuông có 2 cgv là \(x_1,x_2\)là \(\sqrt{x_1^2+x_2^2}=\sqrt{\left(x_1+x_2\right)^2-2x_1x_2}=\sqrt{m^2-2\left(m-1\right)}=\sqrt{m^2-2m+2}\)
Ta có \(x_1x_2=\frac{1}{\sqrt{5}}\sqrt{m^2-2m+2}\)hệ thức lượng trong tam giác vuông.
\(\Leftrightarrow m-1=\frac{1}{\sqrt{5}}\sqrt{m^2-2m+2}\)\(\Leftrightarrow\frac{m-1}{\sqrt{m^2-2m+2}}=\frac{1}{\sqrt{5}}\)\(\Leftrightarrow\sqrt{\frac{m^2-2m+1}{m^2-2m+2}}=\sqrt{\frac{1}{5}}\)\(\Leftrightarrow\frac{m^2-2m+1}{m^2-2m+2}=\frac{1}{5}\)\(\Leftrightarrow5m^2-10m+5=m^2-2m+2\)\(\Leftrightarrow4m^2-8m+3=0\)
\(\Delta_1=\left(-8\right)^2-4.4.3=16>0\)
\(\Rightarrow\orbr{\begin{cases}m_1=\frac{-\left(-8\right)+\sqrt{16}}{2.4}=\frac{3}{2}\\m_2=\frac{-\left(-8\right)-\sqrt{16}}{2.4}=\frac{1}{2}\end{cases}}\)
Vậy để [...] thì \(\orbr{\begin{cases}m=\frac{3}{2}\\m=\frac{1}{2}\end{cases}}\)

Phương trình hoành độ giao điểm:
\(x^2-2\left(m-1\right)x+2m-5=0\) (1)
\(\Delta'=\left(m-1\right)^2-2m+5=\left(m-2\right)^2+2>0;\forall m\)
\(\Rightarrow\) (d) luôn cắt (P) tại 2 điểm pb có hoành độ là nghiệm của (1)
Theo hệ thức Viet \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=2m-5\end{matrix}\right.\)
Theo định lý Pitago:
\(x_1^2+x_2^2=14\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=14\)
\(\Leftrightarrow4\left(m-1\right)^2-2\left(2m-5\right)=14\)
\(\Leftrightarrow4m^2-12m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=3\end{matrix}\right.\)

a) Xét pt hoành độ gđ của (d) và (P):
\(x^2-mx+m-1=0\) (*)
Thay m=4 vào pt (*) => x=3 và x=1 thay vào (P) suy ra được tung độ tương ứng y=9 và y=1
Đ/a: \(\left(3;9\right),\left(1;1\right)\)
b) Để (d) và (P) cắt nhau tại hai điểm pb <=> \(\Delta>0\) <=> \(m^2-4\left(m-1\right)>0\) <=> \(\left(m-2\right)^2>0\) <=> \(m\ne2\)
Theo giả thiết => \(\dfrac{1}{x_1^2}+\dfrac{1}{x_2^2}=\dfrac{1}{\left(\dfrac{1}{\sqrt{5}}\right)^2}\) (Áp dụng hệ thức lượng trong tam giác vuông)
\(\Leftrightarrow\dfrac{x^2_1+x_2^2}{x_1^2.x_2^2}=5\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-5\left(x_1x_2\right)^2=0\)
\(\Leftrightarrow m^2-2\left(m-1\right)-5\left(m-1\right)^2=0\)
\(\Leftrightarrow-4m^2+8m-3=0\) \(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=\dfrac{1}{2}\end{matrix}\right.\)
Vậy...

gọi 2 nghiệm của pt là x1;x2
vì cạnh góc vuông = căn 34 =>tổng bình phương 2 cạnh góc vuông là x12+x22=34 (*)
tìm ra đen ta rôi tim nghiệm theo m thay vô (*) rồi giải pt là ra m thỏa mãn điều kiện
cậu còn cách khác không chứ , tớ đã tính làm cách đó rồi nhưng không khả quan lắm đâu - vì số wá to

GIỜ BÀI NÀY KHÔNG CÒN GIAO LƯU NỮA
(1) (M+1)^2 -2m=m^2 +1 >=0 moi m => (1) được c/m
(2) x1^2 +x^2 =12
=> 4(m+1)^2 -4m =12
m^2+m+1=3 => m=1, -2
=> m
(3) từ (2) GTNN A=3/4 khi x=-1/2
có thể sai đừng tin