Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

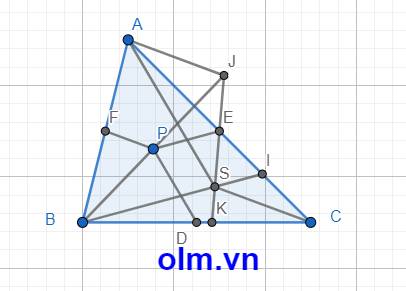
Gọi J là giao điểm của BP và KE; Xét \(\Delta\)BSJ có:
PE // BS; PE = \(\dfrac{1}{2}\) BS
⇒ PF là đường trung bình của \(\Delta\)BSJ (vì đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy)
⇒ PJ = PB; EJ = ES (1)
Xét \(\Delta\)ABJ có: AF = FB (gt); PJ = PB theo (1)
⇒ PF là đường trung bình của \(\Delta\) ABJ (vì đường trung bình của tam giác đi qua trung điểm hai cạnh của tam giác và song song với cạnh còn lại)
⇒ PF// AJ (2)
Xét tứ giác ASCJ ta có: E là giao điểm hai đường chéo
AE = EC (gt)
EJ = ES ( theo (1)
⇒ Tứ giác ASCJ là hình bình hành vì tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ CS // CJ (3)
Kết hợp (2) và(3) ta có:
CS // PF ( vì trong cùng một mặt phẳng hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau.)
Kết luận: nếu BS = 2EP thì CS // PF điều phải chứng minh

a, https://olm.vn/hoi-dap/question/1030999.html
b,\(\frac{\sqrt{3}}{3}\)
CM PD+PE+PF=AH(đường cao)=\(\frac{\sqrt{3}AB}{2}\)
CM BD+CE+AF=\(\frac{3AB}{2}\)
D/s:\(\frac{\sqrt{3}}{3}\)

tự vẽ hình nhé
a)tam giác ABC cân tại A(gt)
=>góc ABC=góc ACB
Xét tam giác BEP có: E thuộc đường trung trực của BP
=>BE=EP
=>tam giác BEP cân tại E
=>góc EBP=góc EPB,mà góc EBP=góc ACB (do góc ABC=góc ACB(cmt))
=>góc EPB=góc ACN,mà chúng ở vị trí đồng vị
=>EP//CF hay EP//AF
Xét tam giác CPF có: F thuộc đường trung trực CP=>CF=PF
=>tam giác CPF cân tại F
=>góc FPC=góc FCP,mà ABC=góc FCP(do góc ABC=góc ACB(cmt))
=>góc FPC=góc ABC,mà chúng ở vị trí đồng vị
=>AB//PF hay AE//PF
Xét tứ giác AEPF có: EP//AF (cmt); AE//PF(cmt)
=>tứ giác AEPF là hình bình hành (DHNB.......)
b, AEPF là hình bình hành (cmt)
=>AF=PE
Lại có CF=PF(cmt)
=>PE + PF = AF + CF = AC không phụ thuộc vào vị trí của điểm P trên BC