Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

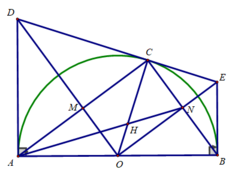
b) Xét tứ giác OMCN có:
∠(OMC) = 90 0 (AC ⊥ OD)
∠(ONC) = 90 0 (CB ⊥ OE)
∠(NCM) = 90 0 (AC ⊥ CB)
⇒ Tứ giác OMCN là hình chữ nhật

a: Xét (O) có
DC,DA là tiếp tuyến
=>DC=DA và OD là phân giác của góc COA
=>OD vuông góc AC
Xét (O) có
EC,EB là tiếp tuyến
=>EB=EC và OE là phân giác của góc COB(2)
=>OE là trung trực của BC
=>OE vuông góc CB
AD+BE=DC+CE=DE
b: Từ (1), (2) suy ra góc DOE=1/2*180=90 độ
Xét tứ giác CMON có
góc CMO=góc CNO=góc MON=90 độ
=>CMON là hình chữ nhật
c: OM*OD+ON*OE
=OC^2+OC^2
=2*R^2ko đổi

a: Xét (O) có
CM,CA là tiếp tuyến
nen CM=CA và OC là phân giác của góc MOA(1)
mà OM=OA
nên OC là trung trực của AM
Xét (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
mà OM=OB
nên OD là trung trực của MB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
b: CD=CM+MD
=>CD=AC+BD
c: Xét tứ giác OEMF có
góc OEM=góc OFM=góc EOF=90 độ
nên OEMF là hình chữ nhật
a: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó:CM=CA
hay C nằm trên đường trung trực của AM(1)
ta có: OA=OM
nên O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra OC là đường trung trực của AM
hay OC⊥AM tại trung điểm của AM
=>K là trung điểm của AM
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB
hay D nằm trên đường trung trực của MB(3)
ta có: OM=OB
nên O nằm trên đường trung trực của MB(4)
Từ (3) và (4) suy ra OD là đường trung trực của MB
=>OD⊥MB và I là trung điểm của MB
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét tứ giác MKOI có \(\widehat{MKO}=\widehat{MIO}=\widehat{IMK}=90^0\)
nên MKOI là hình chữ nhật
b: Xét ΔMAC có
K là trung điểm của MA
I là trung điểm của MB
Do đó: KI là đường trung bình
=>KI//AB
hay KI⊥AC