Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

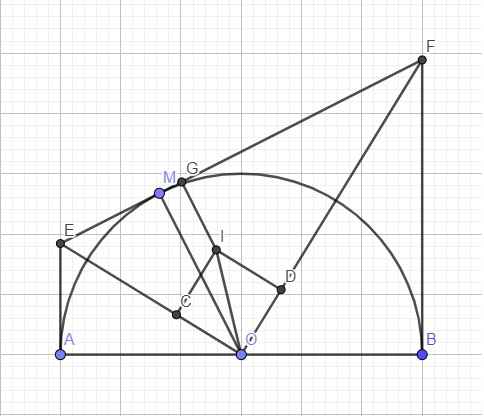
Gọi I là tâm đường tròn nội tiếp EOF, C và D lần lượt là tiếp điểm của (I) với OE và OF
Tứ giác ICOD là hình chữ nhật (có 3 góc vuông)
Mà \(IC=ID=r\Rightarrow ICOD\) là hình vuông
\(S_{IEF}+S_{IEO}+S_{IFO}=\dfrac{1}{2}\left(IG.EF+IC.EO+ID.FO\right)\)
\(=\dfrac{1}{2}r\left(EF+EO+FO\right)\) (do \(IG=IC=ID=r\))
\(=S_{OEF}=\dfrac{1}{2}OM.EF=\dfrac{1}{2}R.EF\)
\(\Rightarrow\dfrac{r}{R}=\dfrac{EF}{EF+OE+OF}>\dfrac{EF}{EF+EF+EF}=\dfrac{1}{3}\)
(do tam giác OEF vuông nên \(OE< EF;OF< EF\))

Giải:
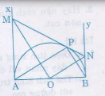
a) Ta có OM, ON lần lượt là tia phân giác cả AOP và BOP
Mà AOP kể bù BOP nên suy ra OM vuông góc với ON.
Vậy ∆MON vuông tại O.
Lại có ∆APB vuông vì có góc vuông (góc nội tiếp chắn nửa cung tròn)
Tứ giác AOPM nội tiếp đường tròn vì có +
= 2v. Nên
=
(cùng chắn cung OP).
Vậy hai tam giác vuông MON à APB đồng dạng vị có cắp góc nhọn bằng nhau.
b)
Tam giác AM = MP, BN = NP (1) (tính chất hai tiếp tuyến cắt nhau)
Tam giác vuông MON có OP là đường cao nên:
MN.PN = OP2 (2)
Từ 1 và 2 suy ra AM.BN = OP2 = R2
c) Từ tam giác MON đồng dạng với tam giác APB ta có :
Khi AM = thi do AM.BN = R2 suy ra BN = 2R
Do đó MN = MP + PN = AM + BN = + 2R =
Suy ra MN2 =
Vậy =
d) Nửa hình tròn APB quay quanh bán kính AB = 2R sinh ra một hình cầu có bán kính R.
Vậy V = πR3

a) vì \(AC\)VÀ \(CM\)LÀ 2 TIẾP TUYẾN CẮT NHAU TẠI \(C\)CỦA ĐƯỜNG TRÒN \(\left(O\right)\)NÊN TA CÓ
- \(CO\)LÀ TIA PHÂN GIÁC \(\widehat{ACM}\) ( TÍCH CHẤT
- \(OC\)LÀ TIA PHÂN GIÁC \(\widehat{AOM}\) 2 TIẾP TUYẾN
- \(AC=CM\) CẮT NHAU )
\(\Rightarrow\widehat{AOC}=\widehat{MOC}\)
C/M TƯƠNG TỰ TA CÓ \(\widehat{MOD}=\widehat{BOD}\)
+ TA CÓ: \(\widehat{AOC}+\widehat{MOC}+\widehat{MOD}+\widehat{BOD}=180^0\)
\(\Leftrightarrow2\widehat{COM}+2\widehat{MOD}=180^0\)
\(\Leftrightarrow2.\left(\widehat{COM}+\widehat{MOD}\right)=180^0\)
\(\Leftrightarrow\widehat{COM}+\widehat{MOD}=90^0\)
HAY \(\widehat{COD}=90^0\)
VẬY \(\widehat{COD}=90^0\)
B) XÉT \(\Delta AOM\)CÓ : \(AO=OM\)( BÁN KÍNH ĐƯỜNG TRÒN TÂM O )
\(\Rightarrow\Delta AOM\)LÀ \(\Delta\)CÂN TẠI O
MÀ \(\widehat{AOI}=\widehat{MOI}\)( TÍNH CHẤT 2 TIẾP TUYẾN CẮT NHAU )
\(\Rightarrow OI\)LÀ TIA PHÂN GIÁC ĐỒNG THỜI LÀ ĐƯỜNG CAO TRONG \(\Delta\) CÂN \(AOM\)
\(\Rightarrow OI\perp AM\)TẠI \(I\)
\(\Rightarrow\widehat{MIO}=90^0\)
C/M TƯƠNG TỰ TA CÓ: \(MK\perp OK\)
\(\Rightarrow\widehat{OKM}=90^0\)
THEO CÂU A) TA CÓ: \(\widehat{COD}=90^0\)
XÉT TỨ GIÁC \(OIMK\) CÓ 3 GÓC VUÔNG \(\Rightarrow\)TỨ GIÁC \(OIMK\)LÀ HÌNH CHỮ NHẬT
VẬY T/G \(OIMK\)LÀ HCN
C) TA CÓ: \(AC=CM\)( TÍNH CHẤT 2 TIẾP TUYẾN ....)
TƯƠNG TỰ \(MD=BD\)
KHI ĐÓ: \(AC.BD\)
\(=CM.MD\)
+ \(OM\perp CM\)( \(CM\)LÀ TIẾP TUYẾN TẠI M )
ÁP DỤNG HỆ THỨC GIỮA CẠNH VÀ ĐƯỜNG CAO VÀO \(\Delta COD\)VUÔGN TẠI \(O\), ĐƯỜNG CAO \(OM\)TA CÓ
\(CM.MD=MO^2\)
\(\Rightarrow CM.MD=R^2\) ( VÌ \(MO\)LÀ BÁN KÍNH)
HAY \(AC.BD=R^2\) MÀ \(R\)KHÔNG ĐỔI
\(\Rightarrow AC.BD\)KO ĐỔI KHI \(C\)DI CHUYỂN TRÊN \(Ax\)
D) VẼ \(I\)LÀ TRUNG ĐIỂM CỦA \(CD\), NỐI \(O\)VỚI \(I\)
\(AC\perp AB\) ( AC LÀ TIẾP TUYẾN TẠI A )
\(BD\perp AB\)( BD LÀ TIẾP TUYẾN TẠI B)
\(\Rightarrow AC\)SONG SONG \(BD\)( CÙNG VUÔNG GOC VỚI AB )
\(\Rightarrow\)T/G \(ACDB\)LÀ HÌNH THANG
XÉT HÌNH THANG \(ACDB\)
CÓ \(CI=DI\)
\(AO=OB\)
\(\Rightarrow OI\)SONG SONG \(AC\)
MÀ \(AC\perp AB\)
\(\Rightarrow OI\perp AB\) ( 1 )
+ \(MC=MD=\frac{1}{2}CD\)
XÉT \(\Delta\)VUÔNG \(COD\)CÓ \(OI\)LÀ ĐƯỜNG TRUNG TUYẾN ỨNG VỚI CẠNH HUYỀN \(CD\)
VÀ \(OI=\frac{1}{2}CD\)
\(\Rightarrow OM=MC=MD\)
\(\Rightarrow M\)CÁCH ĐỀU 3 ĐIỂM \(O,C,D\)
\(\Rightarrow M\in\left(I;\frac{CD}{2}\right)\) ( 2 )
TỪ ( 1 ) VÀ ( 2 ) TA CÓ: \(AB\)LÀ TIẾP TUYẾN CỦA ĐƯỜNG TRÒN ĐƯỜNG KÍNH CD

A B E F x y M K O
a)\(\hept{\begin{cases}Ax⊥AB\\By⊥AB\end{cases}}\)=> Ax // By.\(\Delta KFB\)có EA // FB nên\(\frac{KF}{KA}=\frac{BF}{AE}\)(hệ quả định lí Ta-lét) mà EA = EM ; FM = FB (tính chất của 2 tiếp tuyến)
\(\Rightarrow\Delta AEF\)có\(\frac{KF}{KA}=\frac{MF}{ME}\)nên MK // AE (định lí Ta-lét đảo) mà\(AE⊥AB\Rightarrow MK⊥AB\)
b)\(\widehat{EOM}=\frac{\widehat{AOM}}{2};\widehat{FOM}=\frac{\widehat{MOB}}{2}\)(tính chất 2 tiếp tuyến) mà\(\widehat{EOM}+\widehat{FOM}=180^0\)(kề bù)
\(\Rightarrow\widehat{EOF}=\widehat{EOM}+\widehat{FOM}=\frac{180^0}{2}=90^0\)
\(\Rightarrow\Delta EOF\)vuông tại O có OE + OF > EF (bđt tam giác) ; OE + OF < 2EF (vì OE,OF < EF)
\(\Rightarrow1< \frac{OE+OF}{EF}< 2\Rightarrow2< \frac{P_{EOF}}{EF}< 3\Rightarrow\frac{1}{3}< \frac{EF}{P_{EOF}}< \frac{1}{2}\)(1)
Hình thang AEFB (AE // FB) có diện tích là :\(\frac{\left(AE+FB\right).AB}{2}=\frac{\left(EM+FM\right).2R}{2}=EF.R\)
SAEO = SMEO vì có đáy OA = OM ; đường cao AE = ME\(\Rightarrow S_{MEO}=\frac{1}{2}S_{AEMO}\)
SFOM = SFOB vì có đáy FM = FB ; đường cao OM = OB\(\Rightarrow S_{FOM}=\frac{1}{2}S_{MFBO}\)
\(\Rightarrow S_{EOF}=\frac{1}{2}\left(S_{AEMO}+S_{MFBO}\right)=\frac{EF.R}{2}\).Từ tâm đường tròn nội tiếp I của\(\Delta EOF\)kẻ các đường vuông góc với OE,OF,EF thì\(S_{EOF}=S_{EIF}+S_{EIO}+S_{OIF}\)\(\Leftrightarrow\frac{EF.R}{2}=\frac{EF.r+EO.r+OF.r}{2}\)
\(\Rightarrow EF.R=P_{EOF}.r\Rightarrow\frac{r}{R}=\frac{EF}{P_{EOF}}\)(2).Thay (2) vào (1) ta có đpcm.