

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



vẽ đường tròn ngoại tiếp ngũ giác đều ABCDE
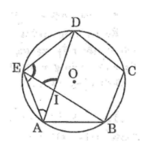

Suy ra tam giác DEI cân tại D ⇒ DI = DE
Mà DE =AE
Nên DI = AE (7)
Từ (4) và (7) suy ra: D I 2 = AI.AD

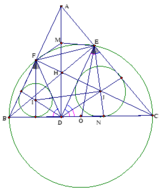
3) Chứng minh EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF
Tứ giác BFEC có B E C ^ = B F C ^ = 90 0
=> tứ giác BFEC nội tiếp đường tròn đường kính BC
Gọi O là tâm đường tròn ngoại tiếp tứ giác BFEC thì O cũng là tâm đường tròn ngoại tiếp tam giác BEF
∆ OBE cân tại O (do OB=OE) => O B E ^ = O E B ^
∆ AEH vuông tại E có EM là trung tuyến ứng với cạnh huyền AH (Vì M là trung điểm AH)
=> ME=AH:2= MH do đó ∆ MHE cân tại M=> M E H ^ = M H E ^ = B H D ^
Mà B H D ^ + O B E ^ = 90 0 ( ∆ HBD vuông tại D)
Nên O E B ^ + M E H ^ = 90 0 Suy ra M E O ^ = 90 0
⇒ E M ⊥ O E tại E thuộc ( O ) => EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF
4) Gọi I và J tương ứng là tâm đường tròn nội tiếp hai tam giác BDF và EDC. Chứng minh DIJ ^ = DFC ^
Tứ giác AFDC có A F C ^ = A D C ^ = 90 0 nên tứ giác AFDC nội tiếp đường tròn => B D F ^ = B A C ^
∆ BDF và ∆ BAC có B D F ^ = B A C ^ (cmt); B ^ chung do đó ∆ BDF ~ ∆ BAC(g-g)
Chứng minh tương tự ta có ∆ DEC ~ ∆ ABC(g-g)
Do đó ∆ DBF ~ ∆ DEC ⇒ B D F ^ = E D C ^ ⇒ B D I ^ = I D F ^ = E D J ^ = J D C ^ ⇒ I D J ^ = F D C ^ (1)
Vì ∆ DBF ~ ∆ DEC (cmt); DI là phân giác, DJ là phân giác ⇒ D I D F = D J D C (2)
Từ (1) và (2) suy ra ∆ DIJ ~ ∆ DFC (c-g-c) => DIJ ^ = DFC ^

a) từ E kẻ đường kính ED' => H thuộc ED' => góc EAD'=90( góc nt chắn nửa đường tròn)
mặt khác ta lại có góc EAD=90( E thuộc AC, D thuộc AB) => D trùng D' => 3 điểm E,H,D thẳng hàng
b) (H): HA=HD=R => tam giác AHD cân => góc HAD=góc HDA
AH là đường cao => góc AHB =90 => góc HAB=góc ACB( cùng phụ góc ABC) hay góc HAD=góc ACB
=> góc HDA=ACB
xét tam giác ABC và tam giác AED: góc A chung, góc HDA=góc ACB => 2 tam giác đồng dạng theo trường hợp g.g
c) tam giác AHM vuông tại H => MH=\(\sqrt{AM^2-AH^2}=\sqrt{5^2-4,8}^2=1,4\)
Tam giác ABC vuông , AM là trung tuyến => MA=MB=MC=5
=> BC=10cm; HC=MC+MH=5+1,4=6,4
HB=MB-MH=5-1,4=3,6
áp dụng hệ thức lượng:
\(AC=\sqrt{BC.HC}=\sqrt{10.6,4}=8\);
từ H kẻ HK vuông góc AB tại K => HK//AC => tam giác ACB đồng dạng tam giác KHB =>\(\frac{KH}{AC}=\frac{HB}{BC}\Leftrightarrow KH=\frac{3,6.8}{10}=2,88\)
S tứ giác AHDM=S MHA+ S AHD
S MHA=1/2 .AH.MH=1/2 .4,8.1,4=3,36.
(H): HA=HD=> HD=5. tam giác AKD vuông tại K=> KD=\(\sqrt{HD^2-HK^2}=\sqrt{5^2-2,88^2}=\sqrt{16,7056}\)
Tam giac AHD cân => HK là đường cao đồng thời là trung tuyến => AD=2KD=\(2\sqrt{16,7056}\)
=> S AHD=1/2.HK.AD=\(\frac{1}{2}.2,88.2\sqrt{16,7056}\)
rồi cộng 2 cái vào là xong nha.
đúng nha. mình làm bài này vừa dài vừa mệt

C D B E A O P K M L Q S T R F N I x
a) Ta thấy: Tứ giác BKQC nội tiếp đường tròn => ^CKQ = ^CBQ (2 góc nội tiếp cùng chắn cung CQ) (1)
Ta có: MK // AD => ^CKM = ^CAD (Đồng vị) . Mà ^CAD = ^CBD (Cùng chắn cung CD) => ^CKM = ^CBD (2)
Từ (1) và (2) => ^CKQ = ^CKM => 2 tia KQ và KM trùng nhau => 3 điểm K,M,Q thẳng hàng (đpcm).
b) Sửa đề: "5 điểm M,S,Q,R,T thẳng hàng ?"
Chứng minh tương tự câu a, ta có: 3 điểm L,M,R thẳng hàng => ^RMQ = ^KML (Đối đỉnh)
Tứ giác AKML là hình bình hành => ^KML = ^KAL = ^CAD. Do đó; ^RMQ = ^CAD (3)
Lại có: ^RTQ = ^RED (Cùng chắn cung RD); ^RED = ^CED = ^CAD => ^RTQ = ^CAD (4)
Từ (3) và (4) => ^RMQ = ^RTQ => Tứ giác RTMQ nội tiếp hay 4 điểm R,T,M,Q thuộc 1 đường tròn (*)
Mặt khác: ^TRS = ^BDE = ^BCE = ^TQS => Tứ giác TRQS nội tiếp hay 4 điểm T,R,Q,S thuộc 1 đường tròn (**)
Từ (*) và (**) => 5 điểm M,S,Q,R,T cùng thuộc 1 đường tròn (đpcm).
c) Giả sử S là 1 điểm chung của (PQR) và (O). Kẻ tia tiếp tuyến Fx của (O). Ta chứng minh Fx cũng là tiếp tuyến của (PQR)
Thật vậy: Gọi giao điểm thứ hai của AF với (PQR) là N. Kéo dài tia AP cắt (O) tại I.
Do L,M,R thẳng hàng; ML // AC => MR // AC => ^RMF = ^CAF (Đồng vị). Mà ^CAF = ^REF
Nên ^RMF = ^REF => Tứ giác EMRF nội tiếp => ^RFM = ^REM hay ^RFN = ^REM
Ta thấy: ^RFN = ^RPN => ^REM = ^RPN. Do 2 góc này đồng vị nên PN // EM hoặc PN // BE (5)
Xét đường tròn (O): 2 dây CD // BE => (BC=(DE => ^BAC = ^EAD
Có ^MAB = ^PAE => ^MAB - ^BAC = ^PAE - ^EAD => ^CAF = ^DAI => (CF=(ID
Xét (O): (CF = (ID, F và I nằm cùng phía so với CD => IF // CD => IF // BE (6)
Từ (5) và (6) => PN // IF => ^FIA = ^NPA (Đồng vị)
Dễ dàng c/m được PF = PI (\(\Delta\)PCF = \(\Delta\)PDI) => ^PIF = ^PFI hay ^FIA = ^PFI
Ta lại có: ^PFx = ^PFI + ^IFx = ^FIA + ^FAI = ^NPA + ^FAI = ^NPA + ^NAP = ^FNP (Góc ngoài)
Mà ^FNP = 1/2.Sđ(FP => ^PFx = 1/2.Sđ(FP => Fx là tia tiếp tuyến của đường tròn (PQR) => Đpcm.
Sorry, "5 điểm M,S,Q,R,T cùng nằm trên 1 đường tròn", mik gõ lộn :(