Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

$(\sqrt{A})^2$ và $\sqrt{A^2}$ khác nhau ở chỗ, ở cái thứ nhất thì bắt buộc điều kiện $A$ phải không âm, để căn thức xác định. Còn cái thứ hai thì $A^2$ luôn không âm rồi nên căn thức xác định với mọi $A$
Vậy, 1 cái thì yêu cầu $A$ luôn không âm từ trước. Một cái $A$ nhận giá trị nào cũng được. Từ đây ta cũng suy ra được:
$(\sqrt{A})^2=A$ không cần dùng trị tuyệt đối vì $A$ đã không âm sẵn rồi.
$\sqrt{A^2}=|A|$ vì không biết $A$ âm hay dương nên phải cho trị tuyệt đối vô để biểu thị căn bậc 2 số học không âm.
Em lưu ý:
- Viết đề bằng công thức toán (biểu tượng $\sum$ bên trái khung soạn thảo) để được hỗ trợ tốt hơn.
- Khi đặt nhiều câu hỏi việc sử dụng dấu "+" đầu dòng nên kết hợp với tách dòng, tách đoạn để câu hỏi trở nên sáng sủa, rõ ràng. Cách đặt câu hỏi em cũng nên lưu ý viết gọn thôi, tập trung vào đúng cái không rõ, không nên dài dòng để câu hỏi được mạch lạc.
Em hiểu đơn giản là em muốn có câu trả lời rõ ràng, mạch lạc thì người trả lời cũng muốn ở em điều ngược lại. Nếu em đặt câu hỏi không được rõ, quá dài thì người đọc sẽ bị ngán hoặc hiểu sai câu hỏi. Do đó, 1 là họ sẽ bỏ qua câu hỏi của em, 2 là họ hiểu lầm nên sẽ có thể không trả lời đúng ý em muốn.

Bạn chỉ cần hiểu là căn bậc hai số học của là một số x sao cho \(x^2=a\) và \(x\ge0\) thôi

Không phải là căn bậc hai số học là đứng độc lập 1 mình đâu bạn
Những trường hợp em nêu đều là CBHSH
$2\sqrt{3}$ là căn bậc 2 số học của $12$
$\sqrt{3}.\sqrt{4}$ là căn bậc 2 số học của $12$
$\sqrt{\frac{3}{4}}$ là căn bậc 2 số học $\frac{3}{4}$
Em cứ nhớ $\sqrt{x}$ (với $x$ là số không âm) là CBHSH của $x$, dù nó biểu diễn kiểu gì đi chăng nữa.

\(1\left(\sqrt{2}+1\right)\left(\sqrt{3}+1\right)\left(\sqrt{6}+1\right)\left(5-2\sqrt{2}-\sqrt{3}\right)\)
\(=1\left(\sqrt{3}+1\right)\left(\sqrt{6}+1\right)\left(1+3\sqrt{2}-\sqrt{6}-\sqrt{3}\right)\)
\(=1\left(\sqrt{6}+1\right)\left(2\sqrt{6}-2\right)\)
\(=2\left(\sqrt{6}-1\right)\left(\sqrt{6}+1\right)=10\)
Cứ nhân lần lược vào rồi rút gọn sẽ được như trên

\(\sqrt{15}-\sqrt{12}=\sqrt{3}\left(\sqrt{5}-\sqrt{4}\right)=\sqrt{3}\left(\sqrt{5}-2\right)\)
Thế vì sao lại đc √3(√5−√4) rồi công thức nào để đc √3(√5−2) ạ


Tại sao không giải ra $\sqrt{P}$ và $\sqrt{P}$?
Em đã có $P$ rồi, nhưng với $\sqrt{P}$, em làm sao rút gọn được khi mà $P$ đã khá gọn rồi. Cũng chẳng có giá trị nào của $x$ để tính cụ thể $P, \sqrt{P}$ rồi đi so sánh. Vì vậy cách này không khả thi.
Vậy thì phải tìm hướng khác. Muốn so sánh 2 số, ta xét hiệu hai số đó.
$P-\sqrt{P}=\sqrt{P}(\sqrt{P}-1)$
Rõ ràng $\sqrt{P}$ đã dương rồi, giờ ta phải xem xét xem $\sqrt{P}-1$ âm hay dương, hay $P$ có lớn hơn 1 không
Đó là lý do vì sao bài giải như trên.
Còn câu hỏi khi nào giải ra từng cái $P$ và $\sqrt{P}$, thì đó là khi đề cho $x=2$ chả hạn, so sánh $P$ và $\sqrt{P}$.
Nhưg hầu như sẽ chẳng có đề nào ra kiểu vậy, mà đa số lợi dụng tính chất của phân thức đó để so sánh (ví dụ như trong bài tính chất nổi bật là $P>1$) cho nhanh. Đó là cái hay của đề bài.

1) Ta có: \(\frac{x+6\sqrt{x}+9}{x-9}=\frac{\left(\sqrt{x}+3\right)^2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\frac{\sqrt{x}+3}{\sqrt{x}-3}\)
 Ai giúp mình giải câu 3 với,mình cảm ơn nhìuuuu ạ 🥺
Ai giúp mình giải câu 3 với,mình cảm ơn nhìuuuu ạ 🥺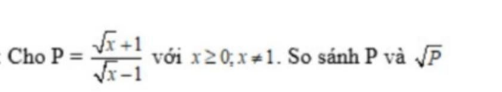
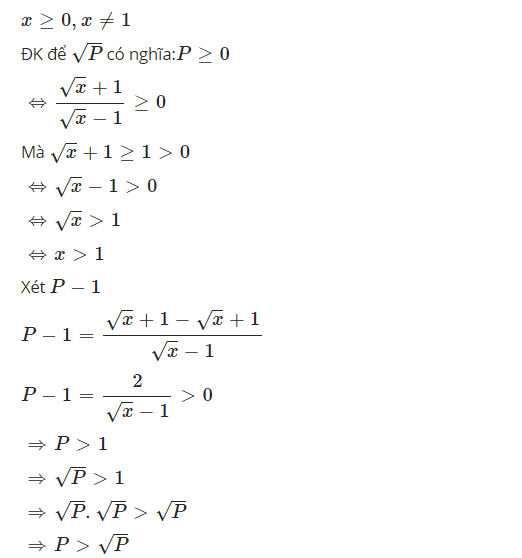
`1/(\sqrt3) = (1.\sqrt3)/(\sqrt3 . \sqrt3) = \sqrt3/3`
\(\dfrac{1}{\sqrt{3}}=\dfrac{1\cdot\sqrt{3}}{\left(\sqrt{3}\right)^2}=\dfrac{\sqrt{3}}{3}\)