A
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
MH
26 tháng 5 2017
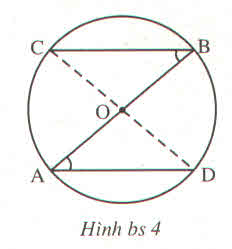
a) Các tam giác cân AOD , BOC có góc đáy bằng nhau nên góc ở đỉnh bằng nhau: \(\widehat{AOD}\) = \(\widehat{BOC}\) . Ta lại có : góc AOD + góc BOD = 180o nên\(\widehat{BOC}\) + \(\widehat{BOD}\) = 180o
Vậy C ,O ,D thẳng hàng
b) Xét tam giác BOC = tam giác AOD (g.c.g)
=> BC = AD (2.c.t.ư)
HN
17 tháng 5 2017
A B C E D F 1 2
a) Vì BC2 = 102 = 100
AB2 + AC2 = 62 + 82 = 100
Nên AB2 + AC2 = BC2
Do đó: \(\Delta ABC\) vuông tại A
b) Xét hai tam giác vuông ABD và EBD có:
BD: cạnh huyền chung
\(\widehat{B_1}=\widehat{B_2}\left(gt\right)\)
Vậy: \(\Delta ABD=\Delta EBD\left(ch-gn\right)\)
Suy ra: DA = DE (hai cạnh tương ứng)
c) \(\Delta DAF\) vuông tại A
=> DF > DA (đường vuông góc ngắn hơn đường xiên)
Mà DA = DE
Do đó: DF > DE (đpcm)
d) Xét hai tam giác vuông ABC và EBF có:
AB = EB (\(\Delta ABD=\Delta EBD\))
\(\widehat{B}\): góc chung
Vậy: \(\Delta ABC=\Delta EBF\left(cgv-gn\right)\)
\(\Rightarrow\) BF = BC (hai cạnh tương ứng)
\(\Rightarrow\) \(\Delta BFC\) cân tại B
\(\Rightarrow\) BD là đường phân giác đồng thời là đường trung trực của FC
Do đó: BD là đường trung trực của đoạn thẳng FC (đpcm).
NT
17 tháng 5 2017
a) Ta có :
\(6^2+8^2=10^2\\ \Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A ( Định lí Pi-ta-go đảo )
b) Xét \(\Delta DBA\) và \(\Delta DBE\),có :
Chung cạnh BD
\(\widehat{DBA}=\widehat{DBE}\)( BD là tia phân giác )
\(\Rightarrow\Delta BDA=\Delta BDE\left(ch-gn\right)\\ \Rightarrow DA=DE\)
SG
1
2 tháng 6 2017
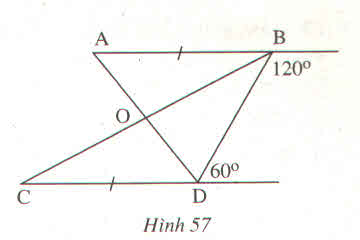
Ta có: góc B + góc D = 1200 + 600 = 1800
Mà hai góc này TCP
=> AB // CD
Xét tam giác ABO và tam giác CDO có:
AB = CD (GT)
ABC = BCD (AB // CD)
BAD = ADC (AB // CD)
=> tam giác ABO = tam giác CDO
=> AO = OD
=> O là trung điểm AD
Ta có: tam giác ABO = tam giác CDO
=> BO = OC
=> O là trung điểm BC
27 tháng 4 2017
thực sự là mình không biết vẽ hình
Chứng minh
a, Xét \(\Delta ABE\) và \(\Delta DBE\) có
BE chung
\(\widehat{BAE}=\widehat{BDE}\) (=1v)
BA = BD (gt)
\(\Rightarrow\Delta ABE=\Delta DBE\left(ch-cgv\right)\)
b, \(\Delta ABE=\Delta DBE\) (câu a )
\(\Rightarrow\widehat{ABE}=\widehat{DBE}\) (hai gó tương ứng)
\(\Rightarrow EA=ED\) (hai cạnh tương ứng) (1)
mà \(\Delta EDC\) vuông tại D
\(\Rightarrow EC>ED\) (2)
Từ (1) và (2) \(\Rightarrow EC>EA\)
Gọi N là giao điểm của AD và BE
Xét \(\Delta ABN\) và \(\Delta DBN\) có :
BA = BD (gt)
\(\widehat{ABN}=\widehat{DBN}\) (c/m trên)
BN chung
\(\Rightarrow\Delta ABN=\Delta DBN\) (c.g.c)
\(\Rightarrow AN=ND\) (hai cạnh tương ứng) (3)
và \(\widehat{ANB}=\widehat{DNB}\) (hai góc tương ứng)
mà \(\widehat{ANB}+\widehat{DNB}=180^O\)
\(\Rightarrow\widehat{ANB}=\widehat{DNB}\) (=1v) (4)
Từ (3) và (4) \(\Rightarrow BE\) là đường trung trực của AD
27 tháng 4 2017
a) xét 2 tam giac vuong ABE va DBE co
AB = BD (gt)
BE canh chung
suy ra: tam giac ABE = tam giac DBE (ch-cgv)
b) tu cau a) Tam giac ABE = tam giac DBE
Suy ra :AE = DE (2 canh tuong ung) (1)_
trong tam giác EDC vuông tại D
suy ra : EC > DE (canh huyen lon hon cach goc vuong ) (2)
Tu (1) va (2) suy ra: EC >EA
Ta co : AE=ED (cmt)
suy ra: E thuộc đường trung trực của AD (3)
ta có:AB=BD(gt)
suy ra: B thuoc duong trung truc AD (4)
tu (3) va (4) suy ra: BE la duong trung truc cua AD
A B C E D M
SG
1
19 tháng 4 2017
a) Trong hình vẽ BE < BC là hai đường xiên vẽ từ B đến đường AC và AE, AC là hai hình chiếu của chúng vì AE < AC nên BE < BC
b) EB và ED là hai đường xiên vẽ từ E đến AB
AB và AD là hai hình chiếu của chúng
Vì AD < AB nên DE < BE
Ta có: BE < BC và DE < BE nên DE < BC
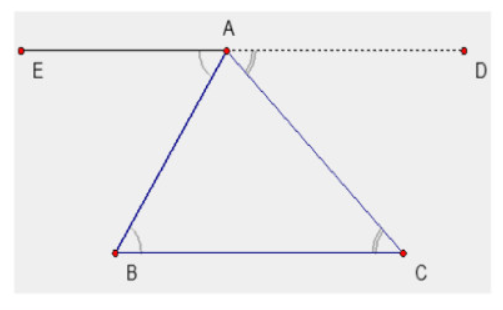
a: Ta có: \(\widehat{EAB}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
Ta có: \(\widehat{DAC}=\widehat{ACB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
b: Ta có: AE//BC
AD//BC
mà AD và AE có điểm chung là A
nên D,A,E thẳng hàng