Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ADE và BCF có:
góc E = góc F=90 độ
AD=BC ( ABCD là hình thang cân)
góc D = góc C
=> tam giác ADE = tam giác BCF (ch-gn)
quá dễ luôn
=> AE=BF ( 2 cạnh tương ứng)

Vì hình thang ABCD cân
AD = BC;
Ĉ = D̂
Xét hai tam giác vuông AED và BFC có:
AD = BC
Ĉ = D̂
⇒ ΔAED = ΔBFC (cạnh huyền – góc nhọn)
⇒ DE = CF.
A B C D E F
Vì tứ giác \(ABCD\)là hình thang cân
\(\Rightarrow\)\(\hept{\begin{cases}AD=BC\\\widehat{ADC}=\widehat{BCD}\end{cases}}\)
Xét \(\Delta AED\)vuông tại \(E\)và \(\Delta BFC\)vuông tại \(F\)có:
\(AD=BC\)( chứng minh trên )
\(\widehat{ADC}=\widehat{BCD}\)( chứng minh trên )
\(\Rightarrow\)\(\Delta AED\)vuông tại \(E\)\(=\) \(\Delta BFC\)vuông tại \(F\)( CH và GN )
\(\Rightarrow\)\(DE=CF\)( hai cạnh tương ứng )

Bài giải:
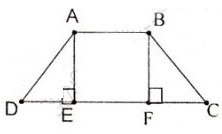
Xét hai tam giác vuông AED và BFC
Ta có: AD = BC (gt)
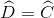 (gt)
(gt)
Nên ∆AED = ∆BFC (cạnh huyền - góc nhọn)
Suy ra: DE = CF

Vì hình thang ABCD cân
AD = BC;
Ĉ = D̂
Xét hai tam giác vuông AED và BFC có:
AD = BC
Ĉ = D̂
⇒ ΔAED = ΔBFC (cạnh huyền – góc nhọn)
⇒ DE = CF.

Vì hình thang ABCD cân
AD = BC;
Ĉ = D̂
Xét hai tam giác vuông AED và BFC có:
AD = BC
Ĉ = D̂
⇒ ΔAED = ΔBFC (cạnh huyền – góc nhọn)
⇒ DE = CF.

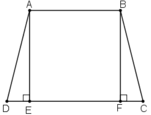
Vì hình thang ABCD cân
AD = BC;
Ĉ = D̂
Xét hai tam giác vuông AED và BFC có:
AD = BC
Ĉ = D̂
⇒ ΔAED = ΔBFC (cạnh huyền – góc nhọn)
⇒ DE = CF.

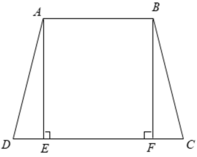
Ta có ABCD là hình thang cân nên AD = BC
+ Xét tam giác vuông ADE có

Xét tứ giác ABFE có AB// EF nên là hình thang. Lại có hai cạnh bên AE// BF (cùng vuông góc CD ) nên AE = BF (3)
Từ ( 1 ), ( 2 ) và ( 3 ) ⇒ DE = CF (do AD = BC và AE = BF )

A B C D E F
Xét 2 tam giác vuông \(\Delta AED\)Và \(\Delta BFC\) CÓ :
\(\widehat{ADE}=\widehat{BCF}\)( Hình thang cân nên 2 góc kề đáy bằng nhau)
\(AD=BC\)( hình tháng cân có 2 cạnh bên bằng nhau )
=> 2 tam giác bằng nhau ( cạnh huyền - góc nhọn )
=> \(DE=CF\)( 2 cạnh tương ứng )