Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Gọi hình bình hành là ABCD và
d:x+ y-1 = 0, ∆: 3x – y+ 5= 0 .
Không làm mất tính tổng quát giả sử
Ta có : 
. Vì I(3;3) là tâm hình bình hành nên C(7;4) ; 
=> Đường thẳng ACcó pt là: x- 4y + 9= 0.
Do 
=> Đường thẳng BC đi qua điểm C và có vtpt 
có pt là: 3x – y- 17= 0.
Khi đó :
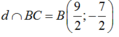
Ta có:
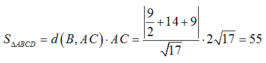
Gọi chiều dài, chiều rộng của hình chữ nhật lần lượt là a và b (a,b>0;m;a>b)
Ta có : (a+b).2=70(m)
\(\Rightarrow\)a+b=35(m)
Ta có :a>b
\(\Rightarrow\)b=\(\frac{3}{4}\)a
Thay b=\(\frac{3}{4}\)a vào a+b=35 ta được :
\(\Leftrightarrow\)\(a+\frac{3}{4}a=35\)
\(\Leftrightarrow\frac{7}{4}a=35\)
\(\Leftrightarrow a=20\left(m\right)\)
\(\Leftrightarrow b=\frac{3}{4}.20=15\left(m\right)\)
Vậy diện tích của hình chữ nhật là :
S=a.b=20.15=300(m2)
BẠN NHỚ TICK VÀ THEO DÕI MK NHÉ
\(AH=\dfrac{2S_{ABC}}{BC}=2\sqrt{5}\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{5}\)
\(\Rightarrow BH=\dfrac{1}{3}BC\)
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{BH}=\dfrac{1}{3}\overrightarrow{BC}\\\overrightarrow{BH}=-\dfrac{1}{3}\overrightarrow{BC}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}H\left(1;1\right)\\H\left(3;-3\right)\end{matrix}\right.\) (sử dụng công thức điểm chia đoạn thẳng theo tỉ lệ)
Gọi G là trọng tâm tam giác\(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
Đặt \(P=MA^2+MB^2+MC^2=\left(\overrightarrow{MG}+\overrightarrow{GA}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GB}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GC}\right)^2\)
\(=3MG^2+GA^2+GB^2+GC^2+2\overrightarrow{MG}\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)
\(=3MG^2+GA^2+GB^2+GC^2\)
Do \(GA^2+GB^2+GC^2\) ko đổi nên \(P_{min}\) khi \(MG_{min}\Leftrightarrow M\) là chân đường vuông góc hạ từ G xuống BC
\(\Rightarrow\dfrac{CM}{BC}=\dfrac{2}{3}\Rightarrow\dfrac{BM}{BC}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{S_{ABM}}{S_{ABC}}=\dfrac{1}{3}\)
Ta có bảng phân bố tần số-tần suất ghép lớp sau:
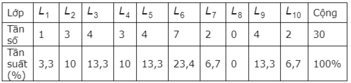
a) Diện tích cột với đáy [45,6;50,4) là ( 50,4 - 45, 6). 4 = 19,2.
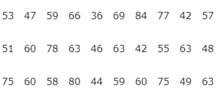
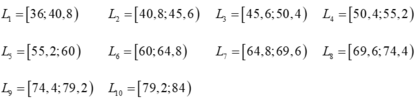
\(S_{ABCD}=S_{ABD}+S_{BCD}\)
\(=\dfrac{1}{2}\left|\left(x_B-x_A\right)\left(y_D-y_A\right)-\left(x_D-x_A\right)\left(y_B-y_A\right)\right|+\dfrac{1}{2}\left|\left(x_C-x_B\right)\left(y_D-y_B\right)-\left(x_D-x_B\right)\left(y_C-y_B\right)\right|\)
\(=\dfrac{1}{2}\left|3.\left(-3\right)-4.4\right|+\dfrac{1}{2}\left|7.\left(-7\right)-1.1\right|=\dfrac{75}{2}\)