Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) E, F là trung điểm AB, CD ⇒ AE = EB = AB/2, DF = FC = CD/2.
Lại có AB = CD = 2.AD = BC.
⇒ AE = EB = BC = CF = FD = DA.
+ Tứ giác ADFE có AE // DF, AE = DF
⇒ ADFE là hình bình hành.
Hình bình hành ADFE có Â = 90º
⇒ ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật có AE= AD
⇒ ADFE là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành
Do đó DE // BF
Tương tự: AF // EC
Suy ra EMFN là hình bình hành
Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.
Hình bình hành EMFN có M̂ = 90º nên là hình chữ nhật.
Lại có ME = MF nên EMFN là hình vuông.

Sai đề bạn ơi..
Sao lại là : " Gọi E ; F lần lượt là trung điểm của BF và CE " ????
bạn sửa lại đi
Vì ABCD là hình chữ nhật (hcn) => EB=CD , AD=BC.
Mà E là trung diểm ( tđ) của AB , F là tđ của DC
=> AE=EB=DF=FC.
mà AB= 2AD ( giả thiết ( gt)) , AE=2AB , AB=DC
=>AD=AE
=> AEFD là hình vuông ( dấu hệu 1 SGK toán 8 trang 107).
b.chứng minh tương tự ta có ABCF là hình vuông.
Ta có 2 hình vuông (hv) AEFD và ABCF có cạnh chung là EF
=> hv AEFD = hv ABCF
Vì 2 hv trên = nhau => AF=FB=CE=DE( các đường chéo = nhau , cắt nhau tại trung điểm mỗi đường)
=> EM=MF=FN=EN (1)
Trong hình vuông , 2 đường chéo vuông góc với nhau
=> EM vuông góc với AF
\(\Rightarrow\widehat{EMF}=90^o\) (2)
Từ (1) và (2) =>EMFN là hình vuông ( đpcm)
mk vẽ hình hơi xấu đó.
.. A B C D E F góc A , góc B , góc C , góc D là các góc vuông

a) Tứ giác ADFE có AE // DF, AE = DF nên là hình bình hành.
Hình bình hành ADFE có góc A = 900 nên là hình chữ nhật.
Hình chữ nhật ADFE có AE = AD nên là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành.
Do đó DE // BF
Tương tự AF // EC
Suy ra EMFN là hình bình hành.
Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.
Hình bình hành EMFN có góc M = 900 nên là hình chữ nhật, lại có ME = MF nên là hình vuông.
a) Tứ giác ADFE có AE // DF, AE = DF nên là hình bình hành.
Hình bình hành ADFE có ˆAA^ = 900 nên là hình chữ nhật.
Hình chữ nhật ADFE có AE = AD nên là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành.
Do đó DE // BF
Tương tự AF // EC
Suy ra EMFN là hình bình hành.
Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.
Hình bình hành EMFN có ˆMM^ = 900 nên là hình chữ nhật, lại có ME = MF nên là hình vuông

a) E, F là trung điểm AB, CD ⇒ AE = EB = AB/2, DF = FC = CD/2.
Lại có AB = CD = 2.AD = BC.
⇒ AE = EB = BC = CF = FD = DA.
+ Tứ giác ADFE có AE // DF, AE = DF
⇒ ADFE là hình bình hành.
Hình bình hành ADFE có Â = 90º
⇒ ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật có AE= AD
⇒ ADFE là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành
Do đó DE // BF
Tương tự: AF // EC
Suy ra EMFN là hình bình hành
Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.
Hình bình hành EMFN có M̂ = 90º nên là hình chữ nhật.
Lại có ME = MF nên EMFN là hình vuông.
A E B D F C M N
a) E, F là trung điểm AB, CD =>.\(AE=EB=\frac{AB}{2},DF=FC=\frac{CD}{2}\)
Ta có: AB = CD = 2AD = 2BC
=> AE = EB = BC = CF = FD = DA.
+ Tứ giác ADFE có AE // DF, AE = DF
=> ADFE là hình bình hành.
Hình bình hành ADFE có \(\widehat{A}=90^o\)
=> ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật có AE= AD
=> ADFE là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành
Do đó DE // BF
Tương tự: AF // EC
Suy ra EMFN là hình bình hành
Theo câu a, ADFE là hình vuông nên ME = MF, \(ME\perp MF\)
Hình bình hành EMFN có \(\widehat{M}=90^o\)nên là hình chữ nhật.
Lại có ME = MF nên EMFN là hình vuông.

a) E, F là trung điểm AB, CD ⇒ AE = EB = AB/2, DF = FC = CD/2.
Lại có AB = CD = 2.AD = BC.
⇒ AE = EB = BC = CF = FD = DA.
+ Tứ giác ADFE có AE // DF, AE = DF
⇒ ADFE là hình bình hành.
Hình bình hành ADFE có Â = 90º
⇒ ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật có AE= AD
⇒ ADFE là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành
Do đó DE // BF
Tương tự: AF // EC
Suy ra EMFN là hình bình hành
Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.
Hình bình hành EMFN có M̂ = 90º nên là hình chữ nhật.
Lại có ME = MF nên EMFN là hình vuông.
M N A B E D F C
a) E, F là trung điểm AB, CD => .\(AE=EB=\frac{AB}{2}\) ; \(DF=FC=\frac{CD}{2}\)
Ta có: AB = CD = 2AD = 2BC
=> AE = EB = BC = CF = FD = DA.
+ Tứ giác ADFE có AE // DF, AE = DF
⇒ ADFE là hình bình hành.
Hình bình hành ADFE có \(\widehat{A}=90^o\)
=> ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật có AE = AD
=> ADFE là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành
Do đó DE // BF
Tương tự: AF // EC
Suy ra EMFN là hình bình hành
Theo câu a, ADFE là hình vuông nên ME = MF, \(ME\perp MF\)
Hình bình hành EMFN có \(\widehat{M}=90^o\)nên là hình chữ nhật.
Lại có ME = MF nên EMFN là hình vuông.

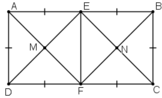
a) E, F là trung điểm AB, CD ⇒ AE = EB = AB/2, DF = FC = CD/2.
Ta có: AB = CD = 2AD = 2BC
⇒ AE = EB = BC = CF = FD = DA.
+ Tứ giác ADFE có AE // DF, AE = DF
⇒ ADFE là hình bình hành.
Hình bình hành ADFE có Â = 90º
⇒ ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật có AE= AD
⇒ ADFE là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành
Do đó DE // BF
Tương tự: AF // EC
Suy ra EMFN là hình bình hành
Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.
Hình bình hành EMFN có M̂ = 90º nên là hình chữ nhật.
Lại có ME = MF nên EMFN là hình vuông.
a: Xét tứ giác ADFE có
AE//DF
AE=DF
Do đó: ADFE là hình bình hành
mà AE=AD
nên ADFE là hình thoi
mà \(\widehat{EAD}=90^0\)
nên ADFE là hình vuông
b: Ta có: ADFE là hình vuông
nên \(\widehat{EFD}=90^0\) và AF vuông góc với DE tại trung điểm của mỗi đường
Xét tứ giác BEFC có
BE//FC
BE=FC
Do đó: BEFC là hình bình hành
mà BC=BE
nên BEFC là hình thoi
mà \(\widehat{EBC}=90^0\)
nên BEFC là hình vuông
=>EC vuông góc với BF tại trung điểm của mỗi đường
Xét ΔEDC có
EF là đường trung tuyến
EF=DC/2
Do đó: ΔEDC vuông tại E
Xét ΔEDC có
EF là đường cao
EF là đường trung tuyến
DO đó: ΔEDC cân tại E
=>ED=EC
=>EM=EN
Xét tứ giác EMFN có \(\widehat{EMF}=\widehat{ENF}=\widehat{MEN}=90^0\)
nên EMFN là hình chữ nhật
mà EM=EN
nên EMFN là hình vuông