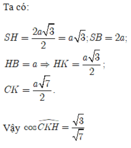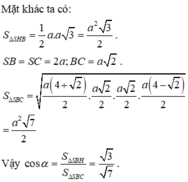Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

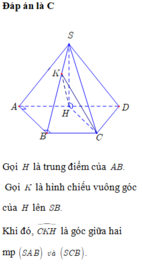
Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\Rightarrow SH\perp\left(ABCD\right)\Rightarrow SH\perp BC\)
Mà \(BC\perp AB\Rightarrow BC\perp\left(SAB\right)\)
Gọi K là trung điểm CD \(\Rightarrow HK||BC\Rightarrow HK\perp AB\Rightarrow HK\perp\left(SAB\right)\)
Trong tam giác SHK, kẻ \(HI\perp SK\Rightarrow HI\perp\left(SCD\right)\)
\(\Rightarrow HI=d\left(H;\left(SCD\right)\right)\)
Mà \(AH||CD\Rightarrow AH||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(H;\left(SCD\right)\right)=HI\)
\(SH=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) ; \(HK=BC=a\)
\(\dfrac{1}{HI^2}=\dfrac{1}{SH^2}+\dfrac{1}{HK^2}=\dfrac{7}{3a^2}\Rightarrow HI=\dfrac{a\sqrt{21}}{7}\)
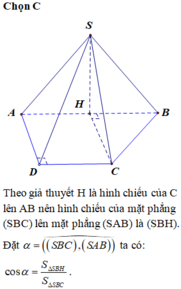
b. Theo cmt ta có \(BC\perp\left(SAB\right)\Rightarrow d\left(C;\left(SAB\right)\right)=BC=a\)
c. \(BC||AD\Rightarrow d\left(C;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Mà BH cắt (SAD) tại A, đồng thời \(BA=2HA\Rightarrow d\left(B;\left(SAD\right)\right)=2d\left(H;\left(SAD\right)\right)\)
Từ H kẻ \(HM\perp SA\Rightarrow HM\perp\left(SAD\right)\Rightarrow HM=d\left(H;\left(SAD\right)\right)\)
\(\dfrac{1}{HM^2}=\dfrac{1}{SH^2}+\dfrac{1}{AH^2}=\dfrac{16}{3a^2}\Rightarrow HM=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow d\left(C;\left(SAD\right)\right)=2HM=\dfrac{a\sqrt{3}}{2}\)

Kẻ SH vuông góc AB tại H.
a, Ta có: \(h=SH=AH.tan\alpha=2a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.2a=\dfrac{8a^3}{3}\)
b, \(SB=BC.tan\alpha=2\sqrt{5}a\Rightarrow SH=\sqrt{SB^2-BH^2}=\sqrt{19}a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.\sqrt{19}a=\dfrac{4\sqrt{19}a^3}{3}\)
c, Kẻ HI vuông góc với CD.
Ta có: \(SH=HI.tan\alpha=6a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.6a=8a^3\)