Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Phương pháp:
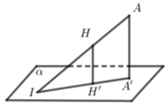
- Xác định góc giữa mặt phẳng (SBD) với (ABD) (góc giữa hai đường thẳng cùng vuông góc với giao tuyến)
- Tính khoảng cách dựa vào công thức tỉ số khoảng cách:
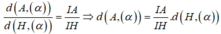
Cách giải
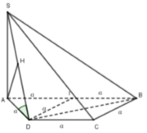




Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
E=AB∩CD,G=EN∩SB⇒GE=AB∩CD,G=EN∩SB⇒G là trọng tâm tam giác SAE.
d(M,(NCD))=GMGBd(B,(NCD))=12d(B,(NCD))=12.12d(A,(NCD))=14d(A,(NCD))=14hd(M,(NCD))=GMGBd(B,(NCD))=12d(B,(NCD))=12.12d(A,(NCD))=14d(A,(NCD))=14h
Tứ diện AEND vuông tại đỉnh A nên 1h2=1AN2+1AE2+1AD2=116a2⇒h=a√66111h2=1AN2+1AE2+1AD2=116a2⇒h=a6611
Vậy d(M,(NCD))=a√6644.d(M,(NCD))=a6644.

a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là giao điểm AC và DI
I là trung điểm AB \(\Rightarrow AI=\dfrac{1}{2}AB=a\Rightarrow AI=DC\)
\(\Rightarrow AICD\) là hình bình hành
Mà \(\widehat{A}=90^0\Rightarrow AICD\) là hình chữ nhật
\(AI=AD=a\) (hai cạnh kề bằng nhau) \(\Rightarrow AICD\) là hình vuông
\(\Rightarrow AC\perp DI\) tại E
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp DI\Rightarrow DI\perp\left(SAE\right)\)
Mà \(DI=\left(SDI\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEA}\) là góc giữa (SDI) và (ABCD)
\(AE=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SEA}\approx50^046'\)

Đề đúng là SC vuông góc (ABCD) phải không nhỉ?
Gọi O là giao điểm AC và BD \(\Rightarrow\) O đồng thời là trung điểm AC và BD
Gọi E và F lần lượt là trung điểm SA và AD, từ O kẻ \(OH\perp EF\) (1)
OE là đường trung bình tam giác SAC \(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}SC=\dfrac{3a}{2}\\OE||SC\Rightarrow OE\perp\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow OE\perp AD\)
OF là đường trung bình tam giác ACD \(\Rightarrow\left\{{}\begin{matrix}OF||CD\Rightarrow OF\perp AD\\OF=\dfrac{1}{2}CD=\dfrac{a}{2}\end{matrix}\right.\)
\(\Rightarrow AD\perp\left(OEF\right)\) \(\Rightarrow AD\perp OH\) (2)
(1);(2) \(\Rightarrow OH\perp\left(SAD\right)\)
\(\Rightarrow HD\) là hình chiếu vuông góc của OD lên (SAD)
\(\Rightarrow\widehat{HDO}\) là góc giữa BD và (SAD)
Hệ thức lượng: \(\dfrac{1}{OH^2}=\dfrac{1}{OE^2}+\dfrac{1}{OF^2}\Rightarrow OH=\dfrac{OE.OF}{\sqrt{OE^2+OF^2}}=\dfrac{3a\sqrt{10}}{20}\)
\(OD=\dfrac{1}{2}BD=\sqrt{AB^2+AD^2}=\dfrac{a\sqrt{5}}{2}\)
\(\Rightarrow sin\widehat{HDO}=\dfrac{OH}{OD}=\dfrac{3\sqrt{2}}{10}\Rightarrow\widehat{HDO}\approx25^06'\)

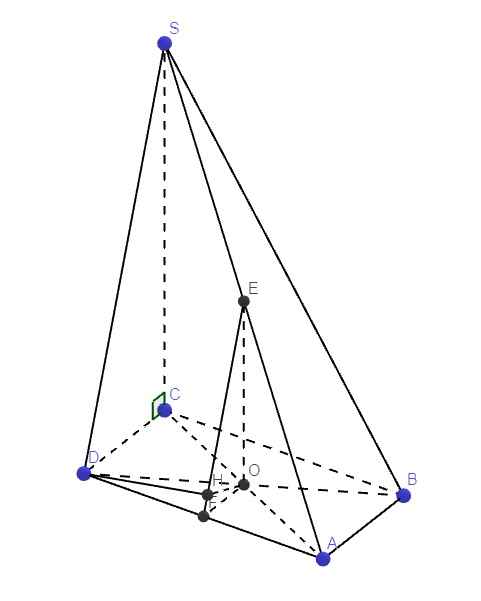
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
\(AC=\sqrt{AD^2+CD^2}=a\sqrt{2}\)
\(BC=\sqrt{BE^2+CE^2}=a\sqrt{2}\)
\(\Rightarrow AC^2+BC^2=AB^2\Rightarrow AC\perp BC\)
\(\Rightarrow BC\perp\left(SAC\right)\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\)
b.
\(CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}=30^0\Rightarrow SA=AD.tan30^0=\dfrac{a\sqrt{3}}{3}\)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
Qua S kẻ đường thẳng d song song AD
Do \(AD||CE\) \(\Rightarrow\) d là giao tuyến (SAD) và (SCE)
Mà \(d\perp\left(SAB\right)\Rightarrow\widehat{ASE}\) là góc giữa (SAD) và (SCE)
\(AE=\dfrac{AB}{2}=a\)
\(tan\widehat{ASE}=\dfrac{AE}{SA}=\sqrt{3}\Rightarrow\widehat{ASE}=60^0\)
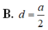
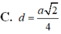
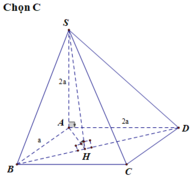

Kẻ \(AF\perp SD\) ; \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp AF\)
\(\Rightarrow AF\perp\left(SCD\right)\)
Kẻ \(AG\perp BD\) ; trong mp (SBD) kẻ \(AH\perp SG\)
\(\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow\widehat{FAH}\) là góc giữa (SCD) và (SBD)
\(AH\perp\left(SBD\right)\Rightarrow AH\perp FH\Rightarrow\Delta FAH\) vuông tại H
Tam giác SAD vuông cân tại A \(\Rightarrow AF=\dfrac{1}{2}SD=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng tam giác SBD: \(\dfrac{1}{AG^2}=\dfrac{1}{AD^2}+\dfrac{1}{AB^2}=\dfrac{5}{4a^2}\)
Hệ thức lượng tam giác SAG: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AG^2}=\dfrac{1}{a^2}+\dfrac{5}{4a^2}=\dfrac{9}{4a^2}\Rightarrow AH=\dfrac{2a}{3}\)
\(\Rightarrow cos\widehat{FAH}=\dfrac{AH}{AF}=\dfrac{2\sqrt{2}}{3}\)
\(\Rightarrow\widehat{FAH}\approx19^028'\)