Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
![]() => Đường thẳng AB có pt là: x- y – 5= 0.
=> Đường thẳng AB có pt là: x- y – 5= 0.
Gọi G(a;3a- 8) suy ra C( 3a- 5; 9a -19).
Ta có:

Vậy C( 1 ; -1) và C( -2 ; 10)

Do O là trung điểm AC \(\Rightarrow\left\{{}\begin{matrix}x_O=\frac{x_A+x_C}{2}\\y_O=\frac{y_A+y_C}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_C=-x_A=-3\\y_C=-y_A=-1\end{matrix}\right.\)
Tương tự: \(\left\{{}\begin{matrix}x_D=-x_B=-1\\y_D=-y_B=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}C\left(-3;-1\right)\\D\left(-1;-2\right)\end{matrix}\right.\)
b/ Ta có \(\overrightarrow{AB}=\left(-2;1\right)\Rightarrow\) đường thẳng AB nhận \(\overrightarrow{n_{AB}}=\left(1;2\right)\) là 1 vtpt
Phương trình AB:
\(1\left(x-3\right)+2\left(y-1\right)=0\Leftrightarrow x+2y-5=0\)
\(\overrightarrow{DA}=\left(4;3\right)\Rightarrow\) đường thẳng AD nhận \(\overrightarrow{n}=\left(3;-4\right)\) là 1 vtpt
Phương trình AD:
\(3\left(x-3\right)-4\left(y-1\right)=0\Rightarrow3x-4y-5=0\)
Hai cạnh còn lại bạn tự viết tương tự

Đáp án B
Gọi hình bình hành là ABCD và
d:x+ y-1 = 0, ∆: 3x – y+ 5= 0 .
Không làm mất tính tổng quát giả sử
![]()
Ta có : ![]() . Vì I(3;3) là tâm hình bình hành nên C(7;4) ;
. Vì I(3;3) là tâm hình bình hành nên C(7;4) ; ![]()
=> Đường thẳng ACcó pt là: x- 4y + 9= 0.
Do ![]() => Đường thẳng BC đi qua điểm C và có vtpt
=> Đường thẳng BC đi qua điểm C và có vtpt ![]() có pt là: 3x – y- 17= 0.
có pt là: 3x – y- 17= 0.
Khi đó :
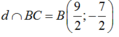
Ta có:
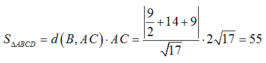

a, Gọi \(I\left(x;y\right)\) là tâm đường tròn ngoại tiếp \(\Delta ABC\)
\(\Rightarrow\left\{{}\begin{matrix}IA=IB\\IA=IC\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}IA^2=IB^2\\IA^2=IC^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-3-x\right)^2+\left(6-y\right)^2=\left(1-x\right)^2+\left(-2-y\right)^2\\\left(-3-x\right)^2+\left(6-y\right)^2=\left(6-x\right)^2+\left(3-y\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2y=-5\\3x-y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)

Câu 1: Chưa đủ dữ kiện để làm. Bạn xem lại đề.
Câu 2: Gọi tọa độ điểm H(a,b)
Ta có: \(\overrightarrow{AH}=(a-3; b-2); \overrightarrow{BC}=(1;8); \overrightarrow{BH}=(a-4; b+1); \overrightarrow{AC}=(2; 5)\)
Vì H là trực tâm tam giác ABC nên:
\(\left\{\begin{matrix} \overrightarrow{AH}.\overrightarrow{BC}=0\\ \overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a-3+8(b-2)=0\\ 2(a-4)+5(b+1)=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} a+8b=19\\ 2a+5b=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{-71}{11}\\ b=\frac{35}{11}\end{matrix}\right.\)

Đáp án A
Giả sử A( x0 ; y0) , Do A ; B đối xứng nhau qua Ox nên B( x0 ; -y0).
Ta có:
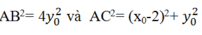
Vì A thuộc (E) nên:
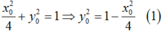
Vì AB = AC nên:
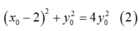
Thay (1) vào (2) ta được:
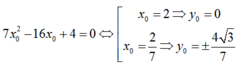
Vì điểm A khác C và Acó tung độ dương nên:
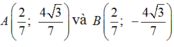

Gọi D \(\left(x_D;y_D\right)\)
\(\overrightarrow{AB}\) = ( 2; 1)
\(\overrightarrow{DC}\) = (5 - \(x_D\); -4 - \(y_D\))
Vì ABCD là hình bình hành
⇔ \(\overrightarrow{AB}=\overrightarrow{DC}\)
⇔ \(\left\{{}\begin{matrix}2=5-x_D\\1=-4-y_D\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_D=3\\y_D=-5\end{matrix}\right.\)
Vậy D ( 3;-5)

\(AH=\dfrac{2S_{ABC}}{BC}=2\sqrt{5}\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{5}\)
\(\Rightarrow BH=\dfrac{1}{3}BC\)
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{BH}=\dfrac{1}{3}\overrightarrow{BC}\\\overrightarrow{BH}=-\dfrac{1}{3}\overrightarrow{BC}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}H\left(1;1\right)\\H\left(3;-3\right)\end{matrix}\right.\) (sử dụng công thức điểm chia đoạn thẳng theo tỉ lệ)
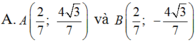
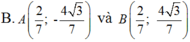
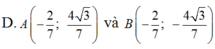
Vì hình bình hành ABCD có tâm I => I là trung điểm của AC và BC
Vì I là trung điểm AC
=> \(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_C}{2}\\y_I=\dfrac{y_A+y_C}{2}\end{matrix}\right.\)
=> xA = -2; yA = 5 => A(-2; 5)
Tương tự ta có D(7; 1)