Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B D C E F O
a)tứ giác ABCD có:BF//ED(vì BC//AD) vàBF=ED(=1/2BC=1/2AD) =>DEBF là hbh.
b)gọi O là giao của 2 đường chéo BD, AC của hbh ABCD.
do đó O là trung điểm BD và AC.(1)
Lại có DEBF là hbh(cmt) => EF giao BD tại trung điểm O của BD.(2)
Từ (1) và(2) suy ra BD,AC và EF đòng quy tại trung điểm O của m,ỗi đường.
a ) Do ABCD là hình bình hành nên AB=CD và AD=BC
Xét \(\Delta ABE\) và \(\Delta CDF\) có :
\(AB=CD\)
\(AE=\frac{1}{2}AD=\frac{1}{2}BC=CF\)
\(\widehat{BAE}=\widehat{DCF}\)
Do đó hai tam giác trên bằng nhau
b,
Từ phần a suy ra \(BE=DF\)
Tứ giác DEBF có 2 cặp cạnh đối BE=DF và DE=BF nên DEBF là hình bình hành
c,
Do ABCD là hình bình hành nên AC và BD là hai đường chéo cắt nhau tại trung điểm mỗi đường
DEBF cũng là hình bình hành nên BD và FE là hai đường chéo cắt nhau tại trung điểm mỗi đường
Do đó AC,DB,FE đồng quy tại O là trung điểm mỗi đường

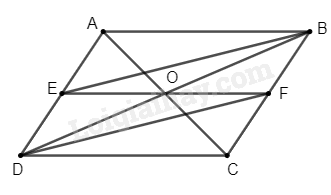
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Mà \(E\), \(F\) là trung điểm của \(AD\), \(BC\) (gt)
Suy ra \(AE = ED = BF = FC\)
Xét tứ giác \(EBFD\) ta có:
\(ED = FB\) (cmt)
\(ED\) // \(BF\) (do \(AD\) // \(BC\))
Suy ra \(EDFB\) là hình bình hành
b) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)
Mà \(DEBF\) là hình bình hành (gt)
Suy ra \(O\) cũng là trung điểm của \(EF\)
Suy ra \(E\), \(O\), \(F\) thẳng hàng

a: Xét tứ giác BEDF có
DE//BF
DE=BF
Do đó: BEDF là hình bình hành
b: Xét ΔAQD có
E là trung điểm của AD
EP//QD
Do đó: P là trung điểm của AQ
Suy ra;AP=PQ(1)
Xét ΔCPB có
F là trung điểm của BC
FQ//BP
Do đó: Q là trung điểm của CP
Suy ra: QC=PQ(2)
Từ (1) và (2) suy ra AP=PQ=QC


a) Tam giác ABE= tam giác CDF
=> EB=DF
b) Ta có:
\(\widehat{ABE}=\widehat{FCD}\)
\(\Rightarrow\widehat{EDF}=\widehat{EBF}=\widehat{BEA}\)
=> EB//CD mà ED//BF
=> EBFD là h.b.h
c) Gọi K là trung điểm EF
=> K là trung điểm AC, BD, EF
=> AC, BD, EF đồng quy tại K