Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy a MQ//NP và MQ=NP
=>MNPQ là hình bình hành
b: Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2 và MN//AC
Để MNPQ là hình chữ nhật thì MN vuông góc với MQ
=>AC vuông góc với BD

Xét tam giác ABC có:
+ M là trung điểm của AB (gt).
+ N là trung điểm của BC (gt).
\(\Rightarrow\) MN là đường trung bình.
\(\Rightarrow\) MN // AC và MN = \(\dfrac{1}{2}\) AC (Tính chất đường trung bình trong tam giác). (1)
Xét tam giác ADC có:
+ Q là trung điểm của DA (gt).
+ P là trung điểm của CD (gt).
\(\Rightarrow\) QP là đường trung bình.
\(\Rightarrow\) QP // AC và QP = \(\dfrac{1}{2}\) AC (Tính chất đường trung bình trong tam giác). (2)
Từ (1); (2) \(\Rightarrow\) MN // QP và MN = QP.
Xét tứ giác MNPQ:
+ MN // QP (cmt).
+ MN = QP (cmt).
\(\Rightarrow\) Tứ giác MNPQ là hình bình hành (dhnb).

o giả thiết cho IJ không song song với CDvà chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K=IJ∩CDK=IJ∩CD.
Ta có : M là điểm chung thứ nhất của (ACD) và (IJM);
{K∈IJIJ⊂(MIJ)⇒K∈(MIJ){K∈IJIJ⊂(MIJ)⇒K∈(MIJ) và {K∈CDCD⊂(ACD)⇒K∈(ACD){K∈CDCD⊂(ACD)⇒K∈(ACD)
Vậy (MIJ)∩(ACD)=MK(MIJ)∩(ACD)=MK
Quảng cáo
b) Với L=JN∩ABL=JN∩AB ta có:
{L∈JNJN⊂(MNJ)⇒L∈(MNJ){L∈JNJN⊂(MNJ)⇒L∈(MNJ)
{L∈ABAB⊂(ABC)⇒L∈(ABC){L∈ABAB⊂(ABC)⇒L∈(ABC)
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P=JL∩AD,Q=PM∩ACP=JL∩AD,Q=PM∩AC
Ta có:
{Q∈PMPM⊂(MNP)⇒Q∈(MNJ){Q∈PMPM⊂(MNP)⇒Q∈(MNJ)
Và {Q∈ACAC⊂(ABC)⇒Q∈(ABC){Q∈ACAC⊂(ABC)⇒Q∈(ABC)
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ=(ABC)∩(MNJ)LQ=(ABC)∩(MNJ).
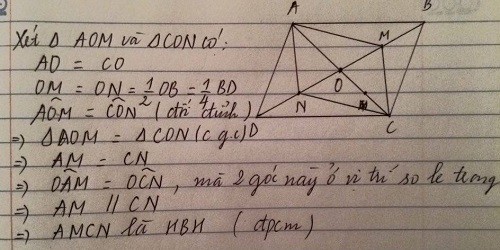
1) Vì ABCD là hình bình hành
=> OA=OC, OB=OD
Ta có: OM=OA/2
OP=OC/2
Mà OA=OC => OM=OP
Cm tương tự ta được OQ=ON
Tứ giác MNPQ có OM=OP. OQ=ON
=> MNPQ là hình bình hành
2) Tứ giác ANCQ có OA=OC (cmt), OQ=ON (cmt)
Suy ra tứ giác ANCQ là hình bình hành
Tứ giác BPDM có OB=OD (cmt), OM=OP (cmt)
Suy ra tứ giác BPDM là hình bình hành