Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thử nhé: Gọi O' là trung điểm của AC.
Tam giác vuông AEC và AFC có trung tuyến lần lượt là EO' và FO' nên O'E=O'F (=1/2AC).
Suy ra: O'EF là tam giác cân. Mà O'M là đường trung tuyến của tam giác O'EF.
nên O'M là đường trung trực của EF.
Vậy O và O' đều là giao điểm của đường trung trực của EF với AC nên O trùng O'. Suy ra O là trung điểm của AC.
Xét tam giác ACH có OA=OC và OM song song AH nên CM=HM.
Xét tứ giác CEHF có 2 đường chéo cắt nhau tại trung điểm mỗi đường nên là hbh. Đến đay làm sao?

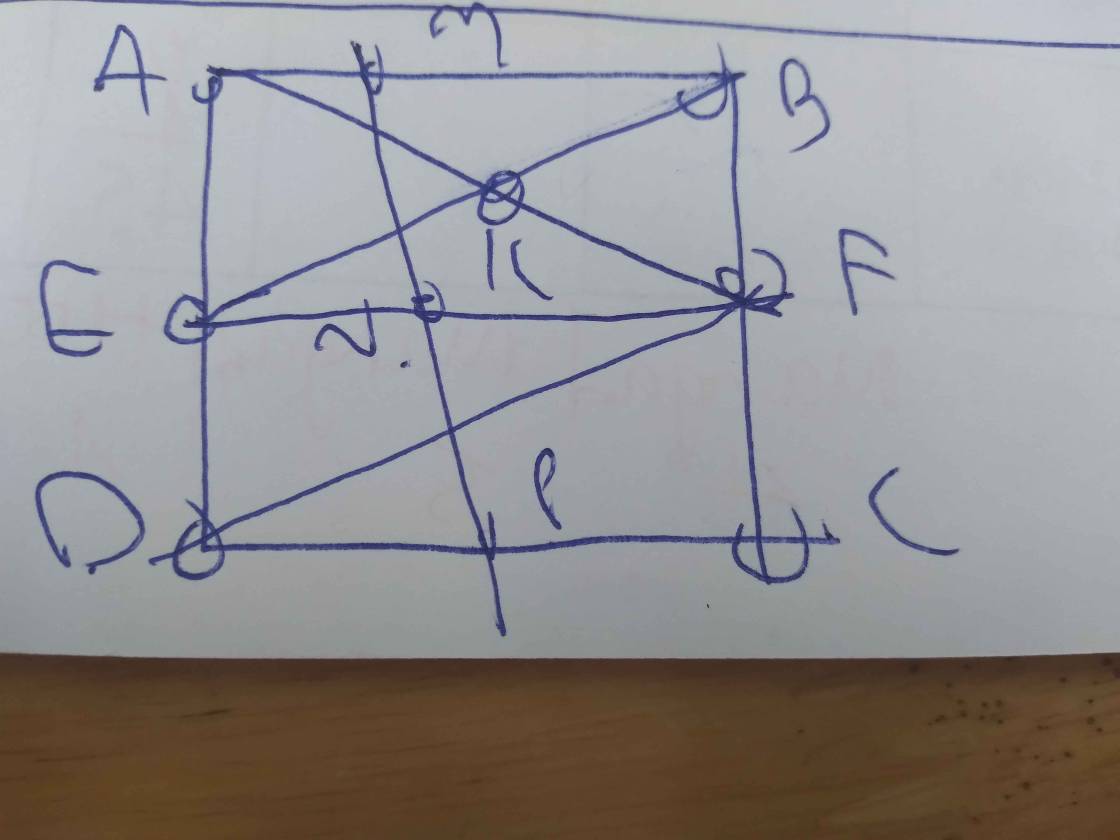
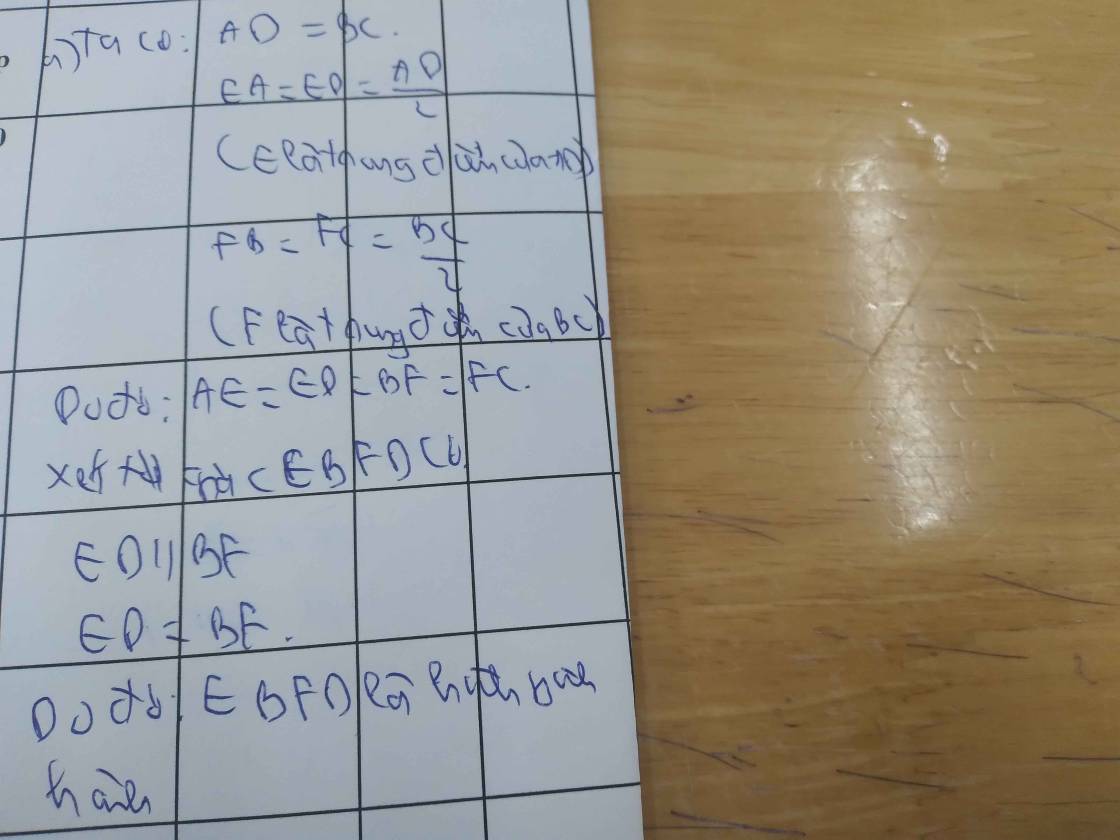
a: Xét tứ giác AEHF có
góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
=>AH=EF
b: góc IFE=90 độ
=>góc IFH+góc EFH=90 độ
=>góc IFH+góc AHF=90 độ
=>góc IFH=góc IHF
=>IH=IF và góc IFC=góc ICF
=>IH=IC
=>I là trung điểm của HC
Xét ΔHAC có HO/HA=HI/HC
nên OI//AC và OI=AC/2
=>OI//AK và OI=AK
=>AOIK là hình bình hành
(((Làm theo hướng đó đúng rồi.. Tiếp nà )))
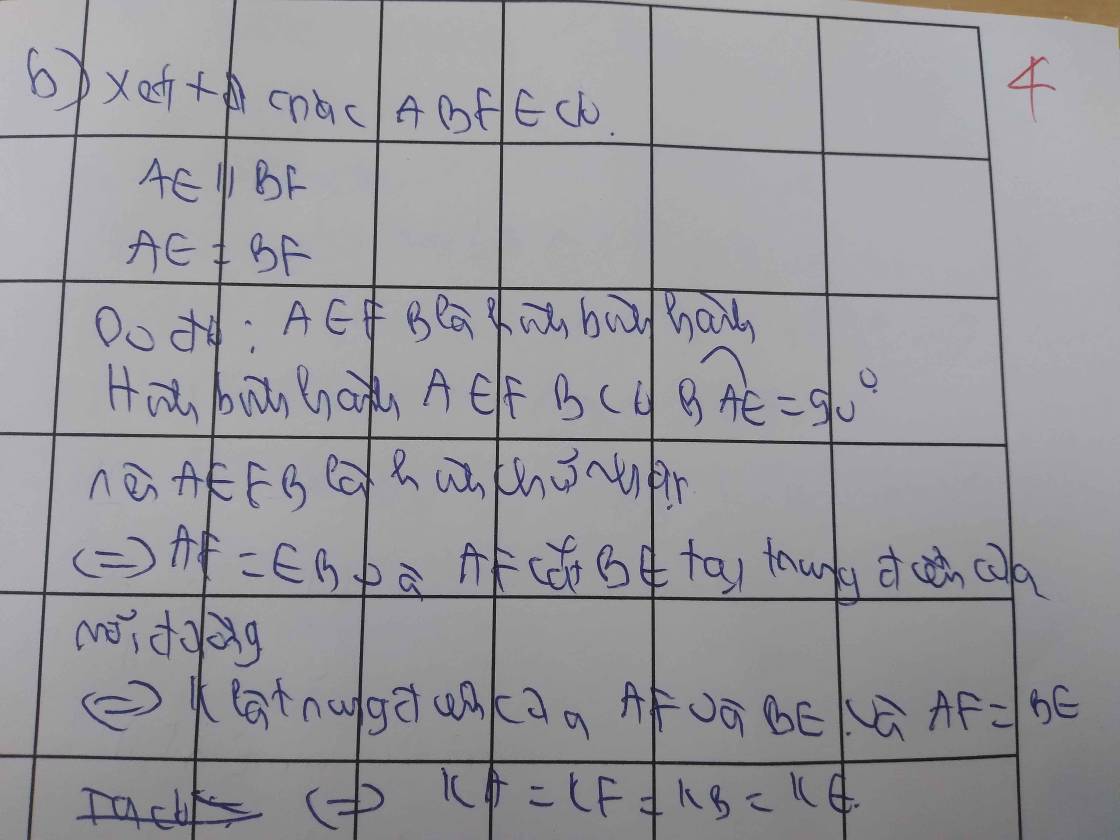
HFCE là hình bình hành (tự c/m)
=> \(\hept{\begin{cases}HF\text{//}EC\\HF=EC\left(1\right)\end{cases}}\)
Mà EC//AK => HF//AK
=> Δ ANK = Δ FNH (g.c.g)
=> AK=HF (2)
Từ (1) và (2) suy ra AK=EC. Mà AK//EC
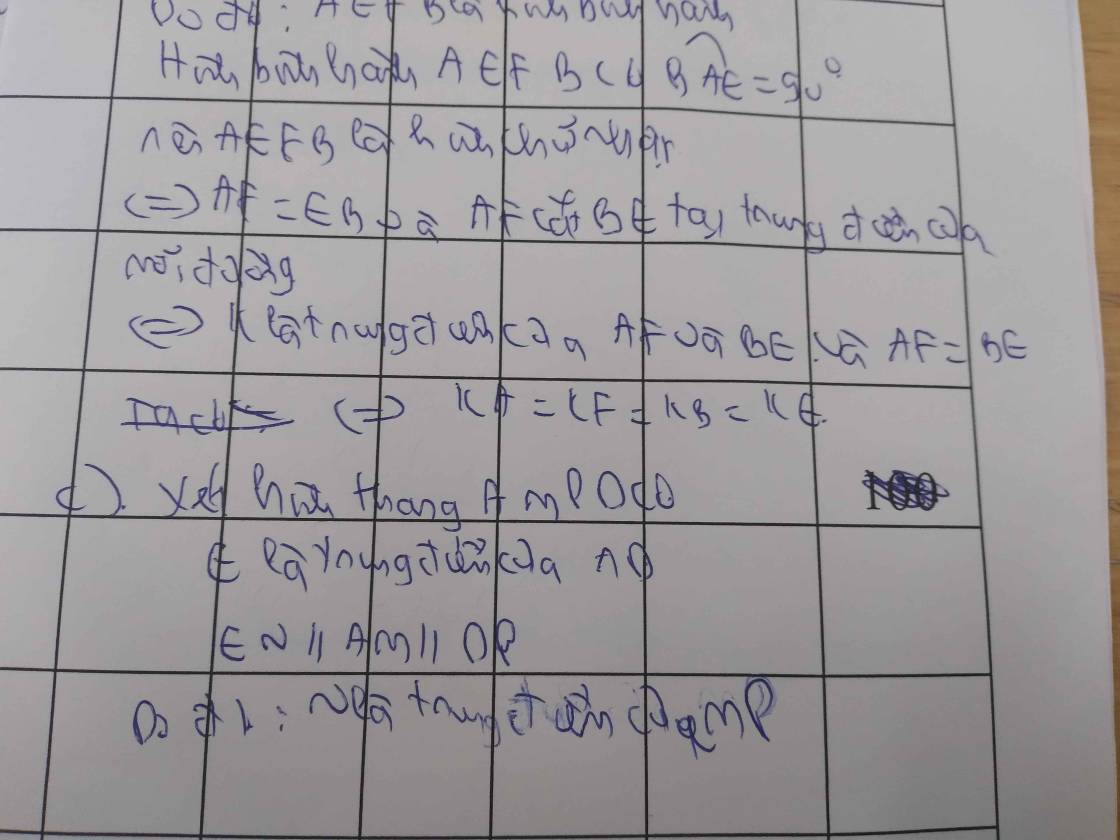
=> Tứ giác AKCE là hình bình hành có O là trung điểm của AC
=> O cũng là trung điểm của EK
=> Đpcm...
Ta thấy : 4 điểm A ; F ; C ; E cùng thuộc đường tròn đường kính AC .
Vì trung trực của EF cắt AC tại O nên O là trung điểm AC .
Ta có : OM , AH cùng vuông góc với EF nên OM // AH
=> M là trung điểm CH ( Vì O là trung điểm của AC )
Do đó , tứ giác CFHE có tâm đối xứng M hay CFHE là hình bình hành .
Suy ra : HF // CE // AK
Dễ chứng minh △HNF = △KNA ( g.c.g )
Suy ra : Tứ giác AHFK là hình bình hành .
Vậy : AK = HF = CE , kết hợp với AK // CE , AK vuông góc với AE .
Suy ra : CKAE là hình chữ nhật .
Vì O là trung điểm đường chéo AC nên O là tâm của hình chữ nhật CKAE hay K , O , E thẳng hàng ( đpcm )