Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2
a. Vì A là giao điểm của 2 đồ thị \(y=-x\) và \(y=-2x+2\) nên tọa độ điểm A là nghiệm của hệ pt: \(\begin{cases}x+y=0\\2x+y=2\end{cases}\) \(\Leftrightarrow\begin{cases}x=2\\y=-2\end{cases}\) vậy \(A\left(2;-2\right)\)
a) y = -x và y = -2x + 2
=> -x = -2x + 2 => -x - (-2x) = 2 => x = 2
=> y = -2
Tọa độ là A(2;-2)
b) Ta có tam giác ABC vuông tại C.
BC = 2 ; AC = 4
Diện tích tam giác ABC là : \(\frac{2.4}{2}=4\) (đơn vị diện tích)
Phương trình hoành độ giao điểm:
\(x^2+2x-m+1=x+1\)
\(\Leftrightarrow x^2+x-m=0\left(1\right)\)
\(\left(d\right),\left(P\right)\) cắt nhau tại hai điểm phân biệt khi phương trình \(\left(1\right)\) có hai nghiệm phân biệt
\(\Leftrightarrow\Delta=4m+1>0\Leftrightarrow m>-\dfrac{1}{4}\)
Phương trình \(\left(1\right)\) có hai nghiệm phân biệt \(x=\dfrac{-1\pm\sqrt{4m+1}}{2}\)
\(x=\dfrac{-1+\sqrt{4m+1}}{2}\Rightarrow y=\dfrac{1+\sqrt{4m+1}}{2}\Rightarrow A\left(\dfrac{-1+\sqrt{4m+1}}{2};\dfrac{1+\sqrt{4m+1}}{2}\right)\)
\(x=\dfrac{-1-\sqrt{4m+1}}{2}\Rightarrow y=\dfrac{1-\sqrt{4m+1}}{2}\Rightarrow B\left(\dfrac{-1-\sqrt{4m+1}}{2};\dfrac{1-\sqrt{4m+1}}{2}\right)\)
\(AB=8\Leftrightarrow\sqrt{8m+2}=8\Leftrightarrow m=\dfrac{31}{4}\left(tm\right)\)
2.
a, \(AB=2\sqrt{5},BC=5\sqrt{10},CA=\sqrt{170}\)
\(AM^2=\dfrac{AB^2+AC^2}{2}-\dfrac{BC^2}{4}=\dfrac{65}{2}\Rightarrow AM=\dfrac{\sqrt{130}}{2}\)
b, \(\left\{{}\begin{matrix}x_D-4-2\left(x_D-2\right)+4\left(x_D+3\right)=0\\y_D-3-2\left(y_D-7\right)+4\left(y_D+8\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_D=-4\\y_D=-\dfrac{14}{3}\end{matrix}\right.\)
\(\Rightarrow D\left(-4;-\dfrac{14}{3}\right)\)
c, \(\left\{{}\begin{matrix}\overrightarrow{AA'}=\left(x_{A'}-4;y_{A'}-3\right)\\\overrightarrow{BC}=\left(-5;-15\right)\\\overrightarrow{BA'}=\left(x_{A'}-2;y_{A'}-7\right)\end{matrix}\right.\)
\(AA'\perp BC\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AA'}.\overrightarrow{BC}=0\left(1\right)\\\overrightarrow{BA'}=k\overrightarrow{BC}\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow-5\left(x_{A'}-4\right)-15\left(y_{A'}-3\right)=0\Leftrightarrow x_{A'}+3y_{A'}=13\)
\(\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}x_{A'}-2=-5k\\y_{A'}-7=-15k\end{matrix}\right.\Leftrightarrow3x_{A'}-y_{A'}=-1\)
\(\left\{{}\begin{matrix}x_{A'}+3y_{A'}=13\\3x_{A'}-y_{A'}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_{A'}=1\\y_{A'}=4\end{matrix}\right.\Rightarrow A'\left(1;4\right)\)
+Ta có 
suy ra đường thẳng AB nhận 
làm vtpt, có phương trình là
1(x-1) +1( y-2) = 0 hay x+ y – 3= 0
+Ta có 
suy ra đường thẳng CD nhận 
làm vtpt, có phương trình là
0 .(x-2) + 1.(y-2) =0 hay y- 2= 0
+Tọa độ giao điểm là nghiệm của hệ phương trình
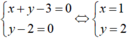
Chọn A
Gọi \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(4;4\right)\\\overrightarrow{DC}=\left(4-x;-1-y\right)\end{matrix}\right.\)
Do \(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow\left\{{}\begin{matrix}4-x=4\\-1-y=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0\\y=-5\end{matrix}\right.\) \(\Rightarrow D\left(0;-5\right)\)
b/ Gọi pt AB có dạng \(y=ax+b\Rightarrow\left\{{}\begin{matrix}-a+b=-2\\3a+b=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-1\end{matrix}\right.\) \(\Rightarrow y=x-1\)
Giao với Ox: \(y=0\Rightarrow x=1\Rightarrow\left(1;0\right)\)
c/ Của đường thẳng y=2 với cái gì bạn?