
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Hàm số \(y=-x^2+2mx+1\) có \(a=-1< 0;-\frac{b}{2a}=m\)nên đồng biến trên \(\left(-\infty;m\right)\)
Do đó để hàm số đồng biến trên khoảng \(\left(-\infty;3\right)\)thì ta phải có \(\left(-\infty;3\right)\subset\left(-\infty;m\right)\Leftrightarrow m\ge3.\)

tròi oi a viết chữ xấu wá đi à, đọc bài của a mà đau mắt wá

\(f\left(x_1\right)-f\left(x_2\right)=\dfrac{x_1^2+\left(m+1\right)x_1+3-x_2^2-\left(m+1\right)x_2-3}{x_1-x_2}\)
\(=\left(x_1+x_2\right)-\left(m+1\right)\)
Vì \(x_1;x_2>1\) nên \(x_1+x_2>2\)
Để hàm số đồng biến trên khoảng \(\left(1;+\infty\right)\) thì \(2-m-1>0\)
=>1-m>0
hay m<1

Mọi \(x_1;x_2\in\left(1;2\right)\)
G/s: \(x_1< x_2\)
Xét \(\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\frac{\left(-x_1^2+\left(m-1\right)x_1+2\right)-\left(-x_2^2+\left(m-1\right)x_2+2\right)}{x_1-x_2}\)
\(=\frac{-\left(x_1^2-x_2^2\right)+\left(m-1\right)\left(x_1-x_2\right)}{\left(x_1-x_2\right)}\)
\(=-\left(x_1+x_2\right)+m-1\)
Để hàm số nghịch biến thì \(\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}< 0\Leftrightarrow m+1< x_1+x_2< 2+2\)=> \(m< 3\)
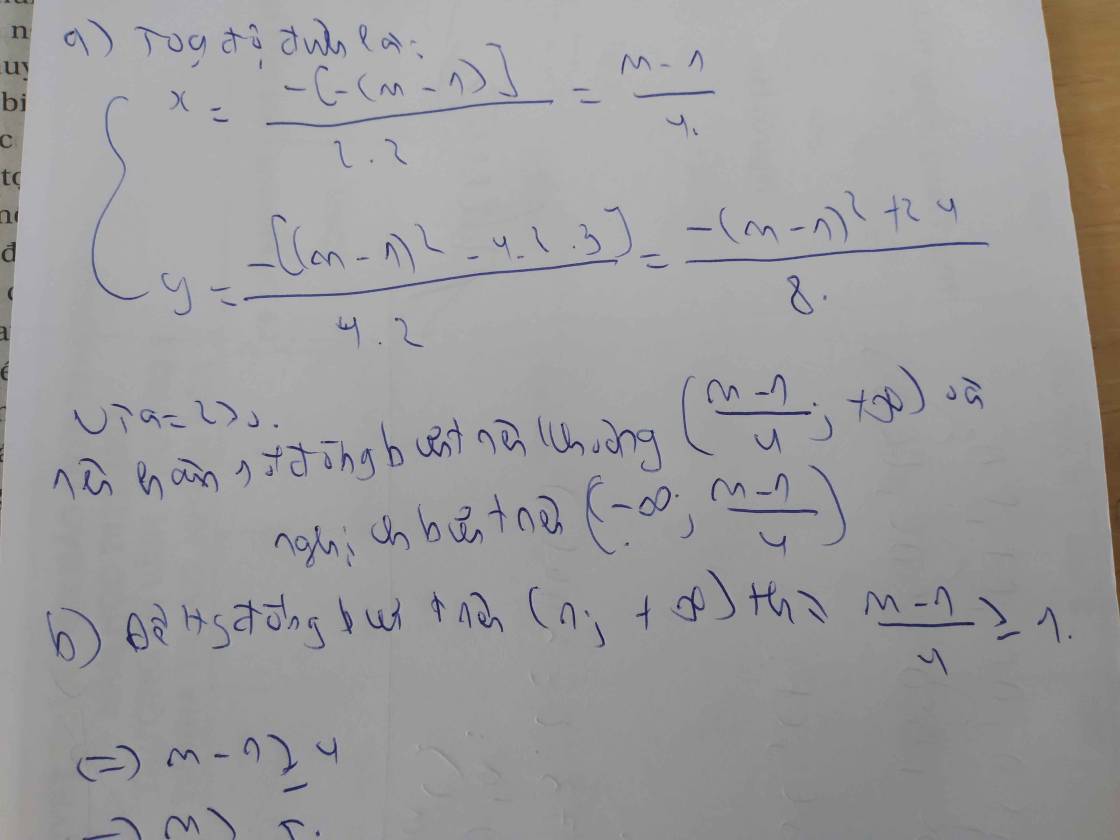

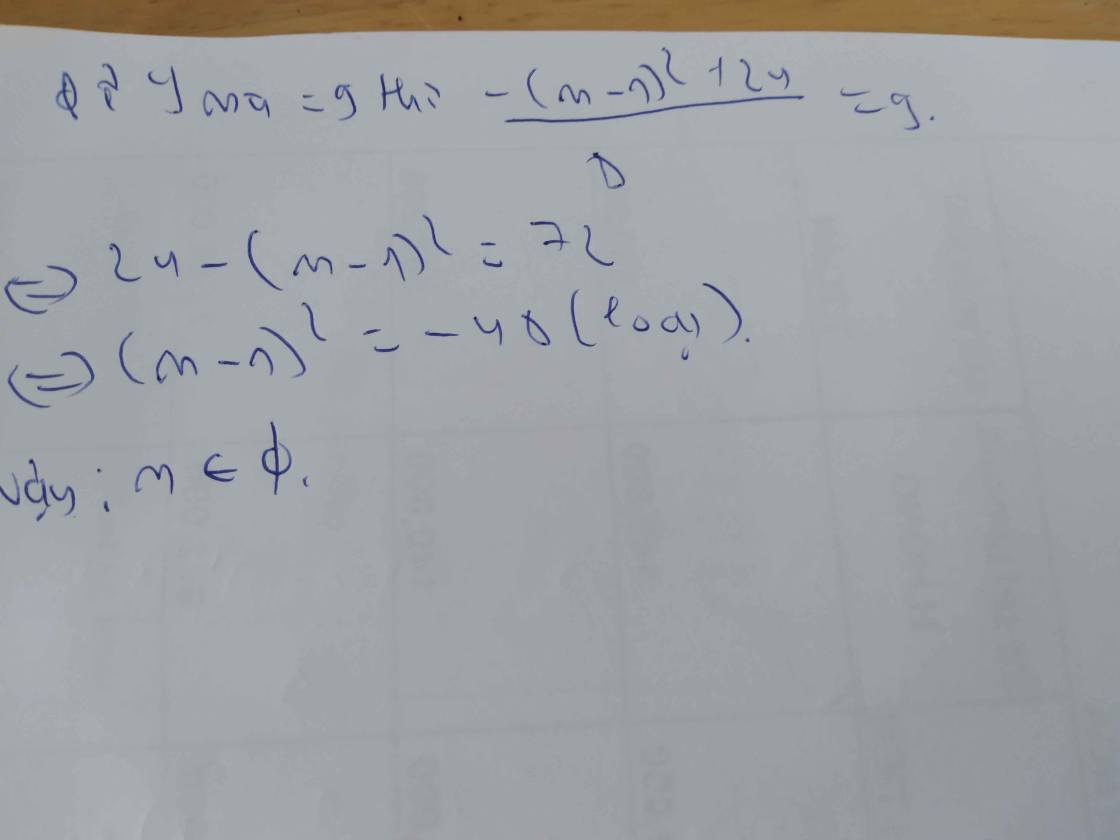
\(a=1>0\) ; \(-\frac{b}{2a}=m-1\Rightarrow\) hàm số đồng biến trên \(\left(m-1;+\infty\right)\)
Để hàm số đồng biến trên \(\left(2;+\infty\right)\)
\(\Leftrightarrow m-1\le2\Rightarrow m\le3\)