Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Thay \({x_1} = - 1;{x_2} = 1\) vào \(y = {x^2}\) ta được:
\({y_1} = f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\({y_2} = f\left( 1 \right) = {1^2} = 1\)
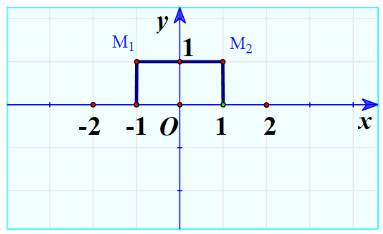
b) Ta có \({x_1} = - 1;{y_1} = 1 \Rightarrow {M_1}\left( { - 1;1} \right)\)
Ta có: \({x_2} = 1;{y_2} = 1 \Rightarrow {M_2}\left( {1;1} \right)\)
Biểu diễn trên mặt phẳng:

b, Ta có : \(0\le x\le1\)
\(\Rightarrow-2\le x-2\le-1< 0\)
Ta có : \(y=f\left(x\right)=2\left(m-1\right)x+\dfrac{m\left(x-2\right)}{\left(2-x\right)}\)
\(=2\left(m-1\right)x-m< 0\)
TH1 : \(m=1\) \(\Leftrightarrow m>0\)
TH2 : \(m\ne1\) \(\Leftrightarrow x< \dfrac{m}{2\left(m-1\right)}\)
Mà \(0\le x\le1\)
\(\Rightarrow\dfrac{m}{2\left(m-1\right)}>1\)
\(\Leftrightarrow\dfrac{m-2\left(m-1\right)}{2\left(m-1\right)}>0\)
\(\Leftrightarrow\dfrac{2-m}{m-1}>0\)
\(\Leftrightarrow1< m< 2\)
Kết hợp TH1 => m > 0
Vậy ...
\(x^2-2\left(m-1\right)x-m^3+\left(m+1\right)^2=0\)
Để pt có hai nghiệm thỏa mãn
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta\ge0\\x_1+x_2=2\left(m-1\right)\le4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\left(m-2\right)\left(m+2\right)\ge0\\m\le3\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}m\in\left[-2;0\right]\cup\left(2;+\infty\right)\cup\left\{2\right\}\\m\le3\end{matrix}\right.\)\(\Rightarrow m\in\left[-2;0\right]\cup\left[2;3\right]\)
\(P=x^3_1+x_2^3+x_1x_2\left(3x_1+3x_2+8\right)\)
\(=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)+3x_1x_1\left(x_1+x_2\right)+8x_1x_2\)
\(=8\left(m-1\right)^3+8\left(-m^3+m^2+2m+1\right)\)
\(=-16m^2+40m\)
Vẽ BBT với \(f\left(m\right)=-16m^2+40m\) ;\(m\in\left[-2;0\right]\cup\left[2;3\right]\)
Tìm được \(f\left(m\right)_{min}=-144\Leftrightarrow m=-2\)
\(f\left(m\right)_{max}=16\Leftrightarrow m=2\)
\(\Rightarrow P_{max}=16;P_{min}=-144\)
Vậy....

Phương trình hoành độ giao điểm là:
\(x^2+mx+\left(m+1\right)^2=-x^2-\left(m+2\right)x-2\left(m+1\right)\)
=>\(x^2+mx+\left(m+1\right)^2+x^2+\left(m+2\right)x+2\left(m+1\right)=0\)
=>\(2x^2+\left(2m+2\right)x+2\left(m+1\right)+\left(m+1\right)^2=0\)
=>\(2x^2+\left(2m+2\right)x+\left(m^2+4m+3\right)=0\)
\(\text{Δ}=\left(2m+2\right)^2-4\cdot2\cdot\left(m^2+4m+3\right)\)
\(=4m^2+8m+4-8m^2-32m-24\)
\(=-4m^2-24m-20\)
\(=-4\left(m^2+6m+5\right)=-4\left(m+1\right)\left(m+5\right)\)
Để (P1) cắt (P2) tại hai điểm phân biệt thì Δ>0
=>\(-4\left(m+1\right)\left(m+5\right)>0\)
=>\(\left(m+1\right)\left(m+5\right)< 0\)
TH1: \(\left\{{}\begin{matrix}m+1>0\\m+5< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-1\\m< -5\end{matrix}\right.\)
=>Loại
TH2: \(\left\{{}\begin{matrix}m+1< 0\\m+5>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< -1\\m>-5\end{matrix}\right.\)
=>-5<m<-1
Theo Vi-et, ta có: \(x_1+x_2=\dfrac{-\left(2m+2\right)}{2}=-m-1;x_1\cdot x_2=\dfrac{c}{a}=\dfrac{m^2+4m+3}{2}\)
\(P=\left|x_1x_2-3\left(x_1+x_2\right)\right|\)
\(=\left|\dfrac{m^2+4m+3}{2}-3\left(-m-1\right)\right|\)
\(=\left|\dfrac{m^2+4m+3}{2}+3m+3\right|\)
\(=\dfrac{\left|m^2+4m+3+6m+6\right|}{2}=\dfrac{\left|m^2+10m+9\right|}{2}\)
Biểu thức này không có giá trị lớn nhất nha bạn
vậy biểu thức này có tìm GTNN được không ạ?
nếu tìm được thì mong bạn giải giùm cho mình được không ạ???

\(\Delta=\left(3m+2\right)^2-12m=9m^2+4>0\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3m-2\\x_1x_2=3m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+1+x_2+1=-3m\\x_1x_2+x_1+x_2+1=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+1+x_2+1=-3m\\\left(x_1+1\right)\left(x_2+1\right)=-1\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}x_1+1=a\\x_2+1=b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a+b=-3m\\ab=-1\end{matrix}\right.\)
\(Q=a^4+b^4\ge2a^2b^2=2\)
Dấu "=" xảy ra khi \(a^2=b^2\Rightarrow\left[{}\begin{matrix}a=b\left(loại\right)\\a=-b\end{matrix}\right.\)
\(\Rightarrow-3m=0\Rightarrow m=0\)

Bài 1:
Khai bút đầu năm lấy may :''>
Đặt $x^2+ax+1=t$ thì ta có hệ \(\left\{\begin{matrix} x^2+ax+(1-t)=0(1)\\ t^2+at+1=0(2)\end{matrix}\right.\)
Trước tiên, pt $(2)$ cần có nghiệm.
Điều này xảy ra khi $\Delta_{(2)}=a^2-4\geq 0\Leftrightarrow a\geq 2$ hoặc $a\leq -2$
Để PT ban đầu có nghiệm duy nhất thì PT $(1)$ phải có nghiệm duy nhất. Điều này xảy ra khi $\Delta_{(1)}=a^2-4(1-t)=0$
$\Leftrightarrow 4(1-t)=a^2$. Mà $a^2\geq 4$ nên $1-t\geq 1\Rightarrow t\leq 0$
------------------
Giờ ta xét:
Nếu $a\leq -2$. Kết hợp với $t\leq 0\Rightarrow at\geq -2t$
$\Rightarrow 0=t^2+at+2\geq t^2-2t+1\Leftrightarrow 0\geq (t-1)^2$.
$\Rightarrow t-1=0\Rightarrow t=1$ (vô lý vì $t\leq 0$)
Do đó $a\geq 2$
Tuy nhiên thay $a=2$ vào hệ ta thấy không thỏa mãn. Do đó $a>2$ (đpcm)
Bài 2:
Nếu $a=0\Rightarrow 2b+5c=0\Rightarow c=\frac{-2}{5}b$
PT trở thành: $bx+c=0$
$\Leftrightarrow bx-\frac{2}{5}b=0$ có nghiệm duy nhất $x=\frac{2}{5}$ nếu $b\neq 0$ hoặc vô số nghiệm nếu $b=0$
Tức là với $a=0$ pt luôn có nghiệm.
Nếu $a\neq 0$. PT đã cho là pt bậc hai ẩn $x$
Xét $\Delta=b^2-4ac=b^2-4(-2b-5c)c=b^2+8bc+20c^2=(b+4c)^2+4c^2\geq 0$ với mọi $b,c$ nên PT đã cho luôn có nghiệm.
Vậy........

\(\Delta=\left(m+2\right)^2-4\left(m^2+1\right)>0\Rightarrow-3m^2+4m>0\Rightarrow0< m< \frac{4}{3}\)
Theo Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=m+2\\x_1x_2=m^2+1\end{matrix}\right.\)
\(A=x_1^3+x_2^3+x_1^2+x_2^2\)
\(=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)+\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(m+2\right)^3-3\left(m^2+1\right)\left(m+2\right)+\left(m+2\right)^2-2\left(m^2+1\right)\)
\(=-2m^3-m^2+13m+4\)
Bạn coi lại đề, biểu thức trên ko có GTLN hay GTNN trên khoảng \(\left(0;\frac{4}{3}\right)\)
a) Ta có:
\(f\left( 1 \right) = 1 + 1 = 2\)
\(f\left( 2 \right) = 2 + 1 = 3\)
\( \Rightarrow f\left( 2 \right) > f\left( 1 \right)\)
b) Ta có:
\(f\left( {{x_1}} \right) = {x_1} + 1;f\left( {{x_2}} \right) = {x_2} + 1\)
\(\begin{array}{l}f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \left( {{x_1} + 1} \right) - \left( {{x_2} + 1} \right)\\ = {x_1} - {x_2} < 0\end{array}\)
Vậy \({x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).