Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/xét OBC và ODA:
-góc O chung
-OD=OB(gt)
-OA=OC(gt) => OBC=ODA =>AD=BC
b/ từ a/ =>gADO = gOBC và gOAD = gOCB =>gBAD=gBCD (bù với 2 g = nhau)
OA=OC và OD=OB => AB=CD
-xét tam giác EAB và ECD:
AB=CD
gBAD=gBCD
gADO=gOBC =>dpcm
c/b/=>ED=EB
xét OBE và ODE: ED=EB
gB=gD
OB=OD =>2 tg = nhau
=>gBOE=gDOE =>OE là p/g
d/gọi M:trung điểm BD
xét tam giác OBM và ODM: OM chung
gBOE=gDOE
OB=OD => 2 tam giác = nhau
=> BM=DM và gBMO=gDMO mà tổng = 180 =>....
e/cm tương tự d/=> OE là trung trực AC
=>gOAC = gOBD (phụ với gBOE) => AC//BD

cái đề dài thế này, chả biết khó hay ko nhưng mà ngại làm quá :[
hình như câu b cho đề sai, pải là: ∆EAB=∆ECD mới đúng

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOBC
nên \(\widehat{OAD}=\widehat{OBC}\)
\(\Leftrightarrow180^0-\widehat{OAD}=180^0-\widehat{OBC}\)
hay \(\widehat{EAB}=\widehat{ECD}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy

a) ∆OAD và ∆OCB có: OA= OC(gt)
=
(=
)
OD=OB(gt)
Nên ∆OAD=∆OCB(c.g.c)
suy ra AD=BC.
b) ∆OAD=∆OCB(cmt)
Suy ra: =
=
=>
=
Do đó ∆AOE = ∆OCE(c .c.c)
suy ra: =
vậy OE là tia phân giác của xOy.
b) ∆AEB= ∆CED(câu b) => EA=EC.
∆OAE và ∆OCE có: OA=OC(gt)
EA=EC(cmt)
OE là cạnh chung.
Nên ∆OAE=∆(OCE)(c .c.c)
suy ra: =
vậy OE là tia phân giác của góc xOy.

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC

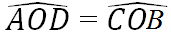
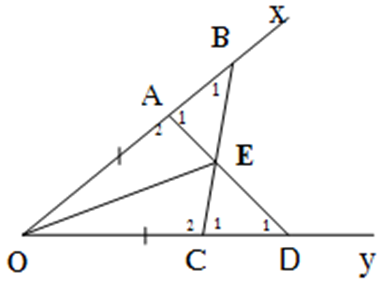
x O y A B C D E I
GỌI I LÀ GIAO ĐIỂM CỦA OE VÀ AC
D) XÉT \(\Delta COI\)VÀ\(\Delta AOI\)CÓ
\(CO=AO\left(GT\right)\)
\(\widehat{COE}=\widehat{IOA}\left(GT\right)\)
\(OI\)LÀ CẠNH CHUNG
\(\Rightarrow\Delta COI=\Delta AOI\left(C-G-C\right)\)
\(\Rightarrow\widehat{CIO}=\widehat{AIO}\)HAI GÓC TƯƠNG ỨNG
MÀ\(\widehat{OIC}+\widehat{OIA}=180^o\left(KB\right)\)
THAY\(\widehat{OIC}+\widehat{OIC}=180^o\)
\(2\widehat{OIC}=180^o\)
\(\widehat{OIC}=180^o:2=90^o\)
nên\(AC\perp OE\)TẠI I
E) CHỨNG MINH TƯƠNG TỰ CÂU D SAU ĐÓ => SO LE TRONG BẰNG NHAU=> //
E) GỌI M LÀ GIAO ĐIỂM CỦA OE VÀDB
VÌ OE LÀ PHÂN GIÁC CỦA GÓC O MÀ OE CŨNG THUỘC GÓC DEB
=> OE CŨNG LÀ TIA PHÂN GIÁC CỦA DEB
XÉT \(\Delta DEM\)VÀ \(\Delta MEB\)CÓ
\(DE=EB\left(\Delta EAB=\Delta ECD\right)\)
\(\widehat{DEM}=\widehat{MEB}\left(CMT\right)\)
EM LÀ CẠNH CHUNG
\(\Rightarrow\Delta DEM=\Delta MEB\left(C-G-C\right)\)
\(\Rightarrow\widehat{DME}=\widehat{EMB}\left(HCTU\right)\)
MÀ\(\widehat{DME}+\widehat{EMB}=180^o\left(kb\right)\)
THAY\(\widehat{DME}+\widehat{DME}=180^o\)
\(2\widehat{DME}=180^o\)
\(\widehat{DME}=180^o:2=90^O\)
\(\Rightarrow\widehat{OIA}=\widehat{DME}=90^O\)
HAI GÓC NÀY Ở VỊ TRÍ ĐỒNG VỊ BẰNG NHAU
\(\Rightarrow AC//BD\)