Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

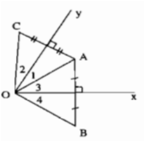
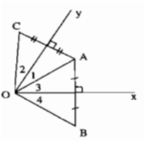
gọi N là giao điểm của BA và Ox
gọi M là giao điểm của AC và Oy
xét tam giác OBN và tam giác OAN có
Góc BNO=góc BNA = 90 độ (Ox là đường trung trực của BA)
BN=BA(Ox là đường trung trực của BA)
ON chung
vậy tam giác OBN =tam giác OAN (ch-cgv)
=>góc BON=góc AON (hai góc tương ứng) (1)
xét tam giácOAM và tam giác OCM có
góc OMA=góc OMC (vì OY là đường trung trực của AC)
AM=CM (vì OY là đường trung trực của AC)
OM chung
vậy tam giácOAM = tam giác OCM (ch-cgv)
=>góc AOM= góc COM (hai góc tương ứng) (2)
từ(1),(2) =>gócBON+góc COM=góc NOA+góc MOC
=>gócBON+góc COM=góc xOy(N thuộc Ox, M thuộc Oy)
=>gócBON+góc COM=60 độ
lại có gócBON+góc COM+góc xOy=góc BOC
hay 6o độ+6o độ=góc BOC
=>góc BOC= 120độ
gọi N là giao điểm của BA và Ox
gọi M là giao điểm của AC và Oy
xét tam giác OBN và tam giác OAN có
Góc BNO=góc BNA = 90 độ (Ox là đường trung trực của BA)
BN=BA(Ox là đường trung trực của BA)
ON chung
vậy tam giác OBN =tam giác OAN (ch-cgv)
=>góc BON=góc AON (hai góc tương ứng) (1)
xét tam giácOAM và tam giác OCM có
góc OMA=góc OMC (vì OY là đường trung trực của AC)
AM=CM (vì OY là đường trung trực của AC)
OM chung vậy tam giácOAM = tam giác OCM (ch-cgv)
=>góc AOM= góc COM (hai góc tương ứng) (2)
từ(1),(2) =>gócBON+góc COM=góc NOA+góc MOC
=>gócBON+góc COM=góc xOy(N thuộc Ox, M thuộc Oy)
=>gócBON+góc COM=60 độ
lại có gócBON+góc COM+góc xOy=góc BOC
hay 6o độ+6o độ=góc BOC
=>góc BOC= 120độ

Câu 1.
Gọi DI là trung trực BC
Xét ΔBIDvà ΔCID:
IDchung
\(\widehat{BDI}=\widehat{CDI}=90^o\)(ID trung trực BC)
BD = CD(như trên)
⇒ΔBID = ΔCID (c.g.c )
⇒ \(\widehat{IBD}=\widehat{C}\)(2gtu)
\(\widehat{B}-\widehat{C}\) = 40
hay \(\widehat{B}-\widehat{IBD}\) = 40
Mà\(\widehat{IBD}+\widehat{ABI}=B\)
\(\Rightarrow\widehat{ABI}=\widehat{B}-\widehat{IBD}=40^o\)

Vì ΔOAB cân tại O và Ox là đường trung trực của AB nên Ox là đường phân giác của ∠(AOB) (tính chất tam giác cân)
Suy ra: ∠O3 = ∠O4 (3)
Vì tam giác OAC cân tại O và Oy là đường trung trực của AC nên Oy là đường phân giác của ∠(AOC) (tính chất tam giác cân)
Suy ra: ∠O1 = ∠O2 (4)
Từ (3) và (4) suy ra: ∠O1 + ∠O3 = ∠O2 + ∠O4
Ta có: ∠(BOC) = ∠O1 + ∠O3 + ∠O2 + ∠O4
= 2(∠O1 + ∠O3 ) = 2.∠(xOy) = 2.60o = 120o.

Vì Ox là đường trung trực của AB nên:
OB = OA (t/chất đường trung trực) (1)
Vì Oy là đường trung trực của AC nên:
OA = OC (t/chất đường trung trực) (2)
Tư (1) và (2) suy ra: OB = OC.