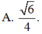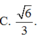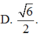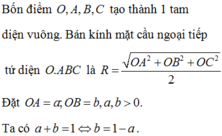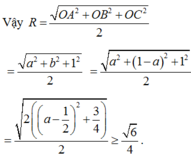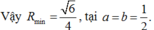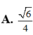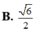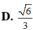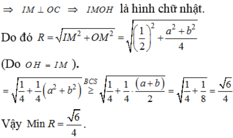Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Sử dụng phương pháp xác định tâm mặt cầu ngoại tiếp khối chóp.
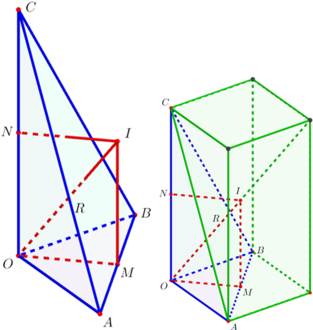
Cách giải: Đặt A(x;0;0), B(0;y;0), (x,y>0)
Vì OA+OB=OC = 1 => x+y=1
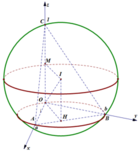
Gọi J, F lần lượt là trung điểm AB, OC. Kẻ đường thẳng qua F song song OJ, đường thẳng qua J song song OC, 2 đường thẳng này cắt nhau tại G
Tam giác OAB vuông tại O => J là tâm đường tròn ngoại tiếp tam giác
![]()
![]()
mà F là trung điểm của OC
=>GF là đường trung trực của OC => GC=GO
=> GO=GA=GB=GC=> G là tâm mặt cầu ngoại tiếp tứ diện OABC.
Bán kính mặt cầu ngoại tiếp tứ diện OABC
![]()
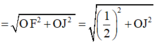
Ta có:
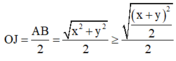
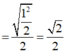
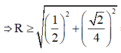
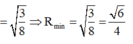

x O y A z u v
a
Do Az//Oy nên \(\widehat{yOA}+\widehat{OAz}=180^0\)
\(\Rightarrow\widehat{OAz}=180^0-35^0=145^0\)
b
Chứng minh cặp góc đồng vị bằng nhau
vì điểm a nằm trong góc xoy nên tia ay nằm giữa tia oc và oy
suy ra xOa +AOy = xOy suy ra xOa =xOy -AOy
thay vào ta có xOa 12độ -75đô=45 độ
vì tia ox nằm giữa tia OA và Ob nên xOa+xOB= AOB
thay vào ta có AOB= 45độ+ 135độ
suy ra AOB =180độ
vậy A,Ô,B thẳng hàng
suy ra AOB = 180độ
vậy A,O,B thẳng hàng

Lớp 7 thôi, đừng cao quá!.
a) \(AC=AE;AB=AD\)
\(\Rightarrow\Delta_VABC\sim\Delta_vADE\left(2cgv\right)\)
b)\(AC=AE\Rightarrow\Delta ACE\) vuông cân tại A.
\(\Rightarrow\widehat{AEC}=\widehat{ACE}=45^o\)
:v thx ạ do đây là lần đâu t hỏi trên đây nên k bt đăng luôn..