Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$

C thay đổi để Uc max thì điện áp uRL vuông pha với u. Ta có giản đồ véc tơ sau:
i U U U=30 O M N J RL C U = 32 L
Xét tam giác vuông OMN:
\(ON^2=NJ.NM\Rightarrow 30^2=(U_C-32).U_C\)
\(\Rightarrow U_C^2-32U_C-30^2=0\)
Giải PT ta được \(U_C=50V\)
Chọn D.
Đặt một điện áp xoay chiều với giá trị hiệu dụng U= 30V vào hai đầu đoạn mạch R, L, C mắc nối tiếp có điện dung C thay đổi được. Khi điện áp hiệu dụng giữa hai bản tụ điện đạt giá trị cực đại UCmax thì hiệu điện thế hiệu dụng giữa hai đầu cuộn cảm là UL = 32V. Giá trị UCmax là
A. 18V
B. 25V
C. 40V
D. 50V

Giải thích: Đáp án C
Phương pháp: Mạch điện R, L, C mắc nối tiếp có ω thay đổi
Cách giải:
+ Khi ω = ω0 công suất trên mạch đạt cực đại 
+ Khi ω = ω1 và ω = ω2 ; ω1 – ω2 = 120π thì công suất tiêu thụ trên đoạn mạch bằng nhau :
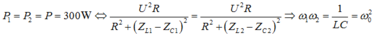
+ Ta có :
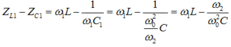
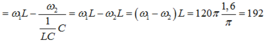
![]()
+ Công suất tiêu thụ : 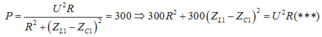
Từ (*) ; (**) ; (***)
![]()

Đáp án A
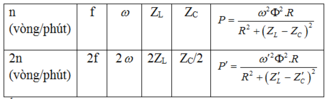
+ Khi tốc độ quay của roto là n (vòng/phút):


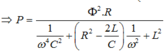
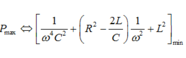
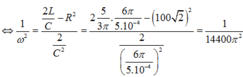
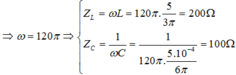
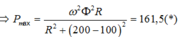
+ Khi tốc độ quay của roto là 2n (vòng/phút)
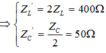
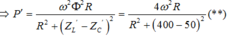
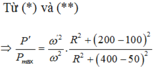
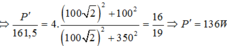

i U U U U U L C R LR RC 3 1
Nhận xét: Do R2 = L/C nên URL vuông pha URC
Không mất tính tổng quát, ta giả sử URL là \(\sqrt{3}\) phần, URC là 1 phần
Từ giản đồ véc tơ, ta có: \(\frac{1}{U_R^2}=\frac{1}{U_{RL}^2}+\frac{1}{U_{RC}^2}=\frac{1}{3}+1=\frac{4}{3}\Rightarrow U_R=\frac{\sqrt{3}}{2}\)
Suy ra: \(U_C=\sqrt{1^2-\left(\frac{\sqrt{3}}{2}\right)^2}=\frac{1}{2}\)
\(U_L=\sqrt{\left(\sqrt{3}\right)^2-\left(\frac{\sqrt{3}}{2}\right)^2}=\frac{3}{2}\)
Vậy \(\cos\varphi=\frac{U_R}{U}=\frac{\frac{\sqrt{3}}{2}}{\sqrt{\left(\frac{\sqrt{3}}{2}\right)^2+\left(\frac{3}{2}-\frac{1}{2}\right)^2}}=\sqrt{\frac{3}{7}}\)

Mạch LC có i vuông qua với q nên:
\((\dfrac{i}{I_0})^2+(\dfrac{q}{Q_0})^2=1\)\(\Rightarrow (\dfrac{i}{\omega Q_0})^2+(\dfrac{q}{Q_0})^2=1\)
\(\Rightarrow (\dfrac{i_1}{\omega Q_0})^2+(\dfrac{q_1}{Q_0})^2=1\)
\((\dfrac{i_2}{\omega Q_0})^2+(\dfrac{q_2}{Q_0})^2=1\)
\(\Rightarrow (\dfrac{i_1}{\omega })^2+(q_1)^2=(\dfrac{i_2}{\omega })^2+(q_2)^2\)
\(\Rightarrow \omega ^2=\dfrac{i_1^2-i_2^2}{q_2^2-q_1^2}\)
\(\Rightarrow T=\dfrac{2\pi}{\omega}=2\pi.\sqrt{\dfrac{q_2^2-q_1^2}{i_1^2-i_2^2}}\)
\(\Rightarrow \lambda = c.T =2\pi c.\sqrt{\dfrac{q_2^2-q_1^2}{i_1^2-i_2^2}}\)
Chọn B.