Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(Z_C=\frac{1}{\omega C}=\frac{1}{2C}\sqrt{LC}=\frac{1}{2}\sqrt{\frac{L}{C}}\)
\(Z_L=\omega L=\frac{2}{\sqrt{LC}}L=2\sqrt{\frac{L}{C}}=4Z_C\)
do uL ngược pha với uc nên uAM ngược pha với uMB \(\Rightarrow\frac{u_{AM}}{u_{MB}}=-\frac{Z_C}{Z_L}=-\frac{1}{4}\Rightarrow u_{MB}=-4.40=-160V\)
Giá trị tức thời điện áp AB bằng tổng giá trị tức thời của điện áp thành phần: uAB = uAM + uMB = 40 - 160 = -120V
@Tuấn: Vì tỉ lệ của U cũng là tỉ lệ của Z mà bạn, nên áp dụng được.

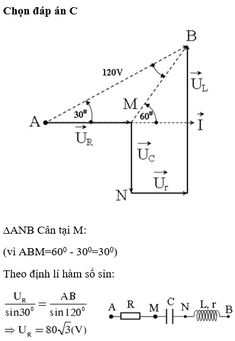
Giải thích: Đáp án C
Theo bài ra ta có U =100√2 V ; ZL=100Ω
Mà
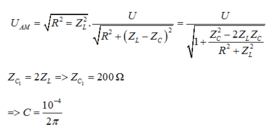

Đáp án D

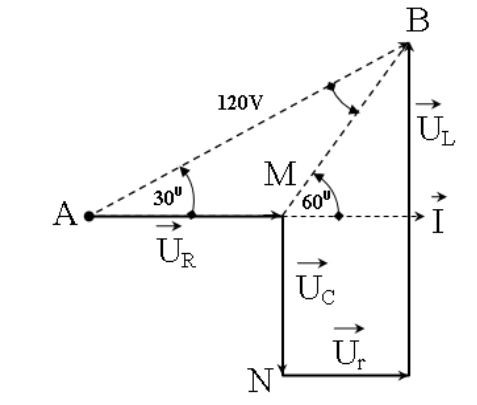
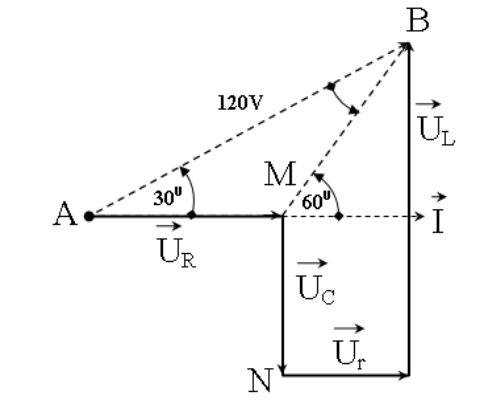
Sử dụng giãn đồ vec tơ ta được:
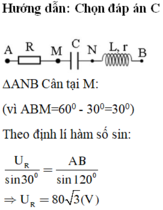
∆ANB cân tại M: (vì góc ABM = 600 - 300 = 300)
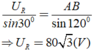

\(U_{AM}^2=U_R^2+U_L^2=40^2\)(1)
\(U_{MB}=U_C=30\) (2)
\(U_{AB}^2=U_R^2+(U_L-U_C)^2=24,15^2\)(3)
Từ (3) \(\Rightarrow U_R^2+U_L^2-2U_LU_C+U_C^2=24,15^2\)
\(\Rightarrow 40^2-2U_L.30+30^2=24,15^2\)
\(\Rightarrow U_L=32V\)
Thay vào (1) suy ra \(U_R\), rồi tính \(\tan\varphi =\dfrac{U_R}{U_L}\)

Từ dữ kiện đề bài ta suy ra cuộn dây có điện trở thuần, với loại bài toán liên quan đến độ lệch pha ta nên vẽ giản đồ véc-tơ:

Ta có: $\widehat{\vec{MB}; \vec{AM}}=60^0$
Mặt khác $\begin{cases} \widehat{\vec{AB};\vec{AM}}=30^0 =\dfrac{1}{2}\widehat{\vec{MB}; \vec{AM}} \\ \widehat{\vec{MB}; \vec{AM}}= \widehat{MAB}+ \widehat{ABM} \end{cases}$
Suy ra $\Delta MAB$ cân tại $M$
Khi đó:
$U_r+U_r=U_{U_{AB}}. \cos 30^0$
Do: $U_r=U_R \cos 60^0$ nên:
$U_R=U_{AM}=\dfrac{U_{AB}\cos 30^0}{1+ \cos 60^0}=80 \sqrt{3} V$