Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O;R) có:
\(\widehat{BCD}\)là góc nt chắn cung BC
\(\widehat{BAC}\)là góc nt chắn cung BC
\(\Rightarrow\widehat{BCD}=\widehat{BAC}=sđ\widebat{BC}\)
Vì dây \(AB\perp CD\)tại M nên \(\widehat{M}=90^o\)
Xét \(\Delta ACM\)và \(\Delta DBM\):
\(\hept{\begin{cases}\widehat{AMC}=\widehat{DMB}=90^o\\\widehat{BAC}=\widehat{BCD}\end{cases}}\)
\(\Rightarrow\Delta ACM\infty\Delta DBM\left(gg\right)\)
\(\Rightarrow\frac{AM}{DM}=\frac{MC}{MB}\Rightarrow AM.MB=MC.DM\)
b) Vì \(\Delta ACM\infty DBM\Rightarrow\widehat{ACM}=\widehat{DBM}\)
Xét \(\left(O;R\right):\)
\(\Delta CDE\)nt (O), cạnh DE là đường kính\(\Rightarrow\Delta CDE\)vuông tại C\(\Rightarrow CD\perp CE\Rightarrow\widehat{DCE}=90^o\)
\(\Delta BDE\)nt \(\left(O\right),\)cạnh DE là đường kính\(\Rightarrow\Delta BDE\)vuông tại B\(\Rightarrow\widehat{DBE}=90^o\)
Có\(\widehat{MAC}+\widehat{ACM}=90^o\Rightarrow\widehat{MAC}=90^o-\widehat{ACM}\)
Và \(\widehat{ABE}+\widehat{DBM}=90^o\Rightarrow\widehat{ABE}=90^o-\widehat{DBM}\)
Mà \(\widehat{ACM}=\widehat{DBM}\)\(\Rightarrow\widehat{MAC}=\widehat{ABE}\)
Do \(AB\perp CD,CD\perp CE\Rightarrow AB//CE\)
Xét tg ABCE có:
\(AB//CE\)
\(\widehat{MAC}=\widehat{ABE}\)
\(\Rightarrow Tg\)ABCE là hthang cân
c) Áp dụng đ/lí Pi-ta-go lần lượt vào các \(\Delta AMC,\Delta BCM;\Delta BDM;\Delta ADM;\Delta BDE\)có:
\(AM^2=AC^2-CM^2\)(1)
\(MB^2=BC^2-CM^2\)(2)
\(MC^2=BC^2-BM^2\)(3)
\(MD^2=BD^2-BM^2\)(4)
\(DE^2=BD^2+BE^2\)(5)
Công từng vế của (1)(2)(3)(4) ta đc đẳng thức:
\(MA^2+MB^2+MC^2+MD^2=AC^2-CM^2+BC^2-CM^2+BC^2-BM^2+BD^2-BM^2\)
\(=AC^2+2BC^2-2CM^2-BM^2+BD^2-BM^2\)
\(=AC^2+2BM^2-BM^2+BD^2-BM^2\)(vì \(BM^2=BC^2-CM^2\))
\(=AC^2+BD^2\)
\(=BE^2+BD^2\)(vì AC=BE do ABCE là hthang cân)
\(=DE^2\)(c/m (5))
Mà DE là đường kính của (O) nên DE=2R\(\Rightarrow DE^2=\left(2R\right)^2=4R^2\)
Vậy \(MA^2+MB^2+MC^2+MD^2\)có g/trị ko đổi khi M thay đổi trong (O)

A B C D M E O
Gọi E là điểm đối xứng với C qua tâm O của đường tròn
Dễ dàng chứng minh được ABED là hình thang cân.
=> BD = AE
Ta có : \(MA^2+MB^2+MC^2+MD^2=\left(MA^2+MC^2\right)+\left(MB^2+MD^2\right)=AC^2+BD^2\)
\(=AC^2+AE^2=CE^2=\left(2R\right)^2=4R^2\) KHÔNG ĐỔI.

\(MA.MB=MC.MD\Leftrightarrow\Delta MAC\approx\Delta MDB\left(G-G\right)\)
Duong thang OM cat duong tron tai E,F
chung minh tuong tu ta co \(MA.MB=ME.MF=\left(R-d\right)\left(R+d\right)=R^2-d^2\)

O A C B D I M N E F P H
a) Kẻ đường kính DP của (O), ta có: BD vuông góc BP. Mà BD vuông góc AC nên BP // AC
=> (AP = (BC => (AB = (CP => AB = CP => AB2 + CD2 = CP2 + CD2 = DP2 = 4R2 (ĐL Pytagore)
Tương tự: AD2 + BC2 = 4R2 => ĐPCM.
b) Ta có: AB2 + BC2 + CD2 + DA2 = 4R2 + 4R2 = 8R2
Ta lại có: AC2 + BD2 = IA2 + IB2 + IC2 + ID2 + 2.IB.ID + 2.IA.IC = AB2 + CD2 + 4.IE.IF
= 4R2 + 4(R+d)(R-d) = 4R2 + 4R2 - 4d2 = 8R2 - 4d2
c) Gọi tia NI cắt AB tại H. Dễ thấy: ^BIH = ^NID = ^NDI = ^IAB = 900 - ^IBA => IN vuông góc AB.
C/m tương tự, ta có: IM vuông góc CD => ĐPCM.
d) Đường tròn (O): Dây AB, M trung điểm AB => OM vuông góc AB. Mà AB vuông góc IN => OM // IN
Tương tự ON // IM. Do đó: Tứ giác OMIN là hình bình hành (đpcm).
e) Vì tứ giác OMIN là hình bình hành nên MN đi qua trung điểm OI. Mà OI cố định NÊN trung điểm của OI cũng cố định nên ta có đpcm.
Chậc -_- bài này mình làm được lâu rồi bạn à :V Nhưng cũng cảm ơn , tớ nhờ cậu bài khác mà :(

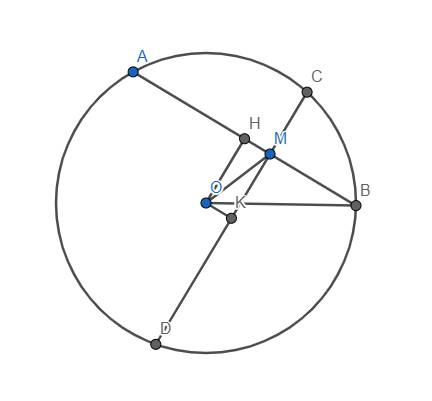
Hạ \(OH\perp AB\), \(OK\perp CD\). Dễ thấy tứ giác OHMK là hình chữ nhật \(\Rightarrow HK=OM\)
Lại có \(AB^2=4HB^2=4\left(OB^2-OH^2\right)=4R^2-4OH^2\) (1)
và \(CD^2=4CK^2=4\left(OC^2-OK^2\right)=4R^2-4OK^2\) (2)
Từ (1) và (2), suy ra \(AB^2+CD^2=8R^2-4\left(OH^2+OK^2\right)\) \(=8R^2-4HK^2=8R^2-4OM^2\) không đổi, đpcm.

a)
Từ M kẻ tiếp tuyến Mx của (O) nên OA vuông góc với Mx
Ta có tứ giác MEHF là tứ giác nội tiếp => góc MFE=góc MHE(1)
Mà góc MHE=góc MAH(2) (+góc HMA=90o)
Từ (1) và (2) => góc MAB = góc MFE
Mặt khác góc MAB=góc BMx (=1/2 số đo cung MB )
=>EF song song với Mx
Om vuông góc Mx => OM vuông góc È
mà MD vuông góc È => o thuộc MD => dpcm
