Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO⊥AB
mà ΔOAB cân tại O
nên K là trung điểm của AB

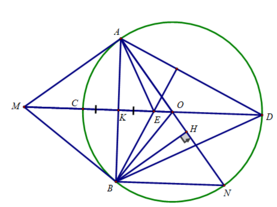
a) Ta có:
MA = MB ( tính chất 2 tiếp tuyến cắt nhau)
OA = OB ( cùng bằng bán kính đường tròn (O)
⇒ OM là đường trung trực của AB
OM ∩ AB = K ⇒ K là trung điểm của AB

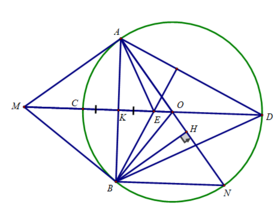
d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB

a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của BA(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại trung điểm H của AB
b: Xét (O) có
\(\widehat{MAP}\) là góc tạo bởi tiếp tuyến AM và dây cung AP
\(\widehat{AQP}\) là góc nội tiếp chắn cung AP
Do đó: \(\widehat{MAP}=\widehat{AQP}\)
=>\(\widehat{MAP}=\widehat{MQA}\)
Xét ΔMAP và ΔMQA có
\(\widehat{MAP}=\widehat{MQA}\)
\(\widehat{AMP}\) chung
Do đó: ΔMAP đồng dạng với ΔMQA
=>\(\dfrac{MA}{MQ}=\dfrac{AP}{QA}\left(1\right)\)
Xét (O) có
ΔQAP nội tiếp
QP là đường kính
Do đó: ΔQAP vuông tại A
Xét ΔHAP vuông tại H và ΔHQA vuông tại H có
\(\widehat{HAP}=\widehat{HQA}\left(=90^0-\widehat{HPA}\right)\)
Do đó: ΔHAP đồng dạng với ΔHQA
=>\(\dfrac{HA}{HQ}=\dfrac{AP}{QA}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{MA}{MQ}=\dfrac{HA}{HQ}\)
=>\(MA\cdot HQ=MQ\cdot HA\)

Mình làm tắt nha bạn không hiểu đâu thì hỏi lại nhé
a) MA, MB là tiếp tuyến
=> \(\widehat{OBM}=\widehat{OAM}=90^o\) (t/c tiếp tuyến)
=> \(\widehat{OBM}+\widehat{OAM}=180^o\)
mà 2 góc đối nhau
=> tứ giác AOBM nội tiếp
=> 4 điểm A, O, B, M cùng thuộc 1 đường tròn
b) Áp dụng hệ thức lượng vào tam giác OAM vuông tại A đường cao AH
=> \(AM^2=MH.MO\)
Áp dụng hệ thức lượng vào tam giác DAM vuông tại A đường cao AC
=> \(AM^2=MC.MD\)
=> \(AM^2=MH.MO=MC.MD\)
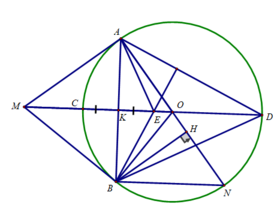
c) Ta có: ∠(ABN ) = 90 0 (B thuộc đường tròn đường kính AN)
⇒ BN // MO ( cùng vuông góc với AB)
Do đó:
∠(AOM) = ∠(ANB) (đồng vị))
∠(AOM) = ∠(BOM) (OM là phân giác ∠(AOB))
⇒ ∠(ANB) = ∠(BOM)
Xét ΔBHN và ΔMBO có:
∠(BHN) = ∠(MBO ) = 90 0
∠(ANB) = ∠(BOM)
⇒ ΔBHN ∼ ΔMBO (g.g)
Hay MB. BN = BH. MO