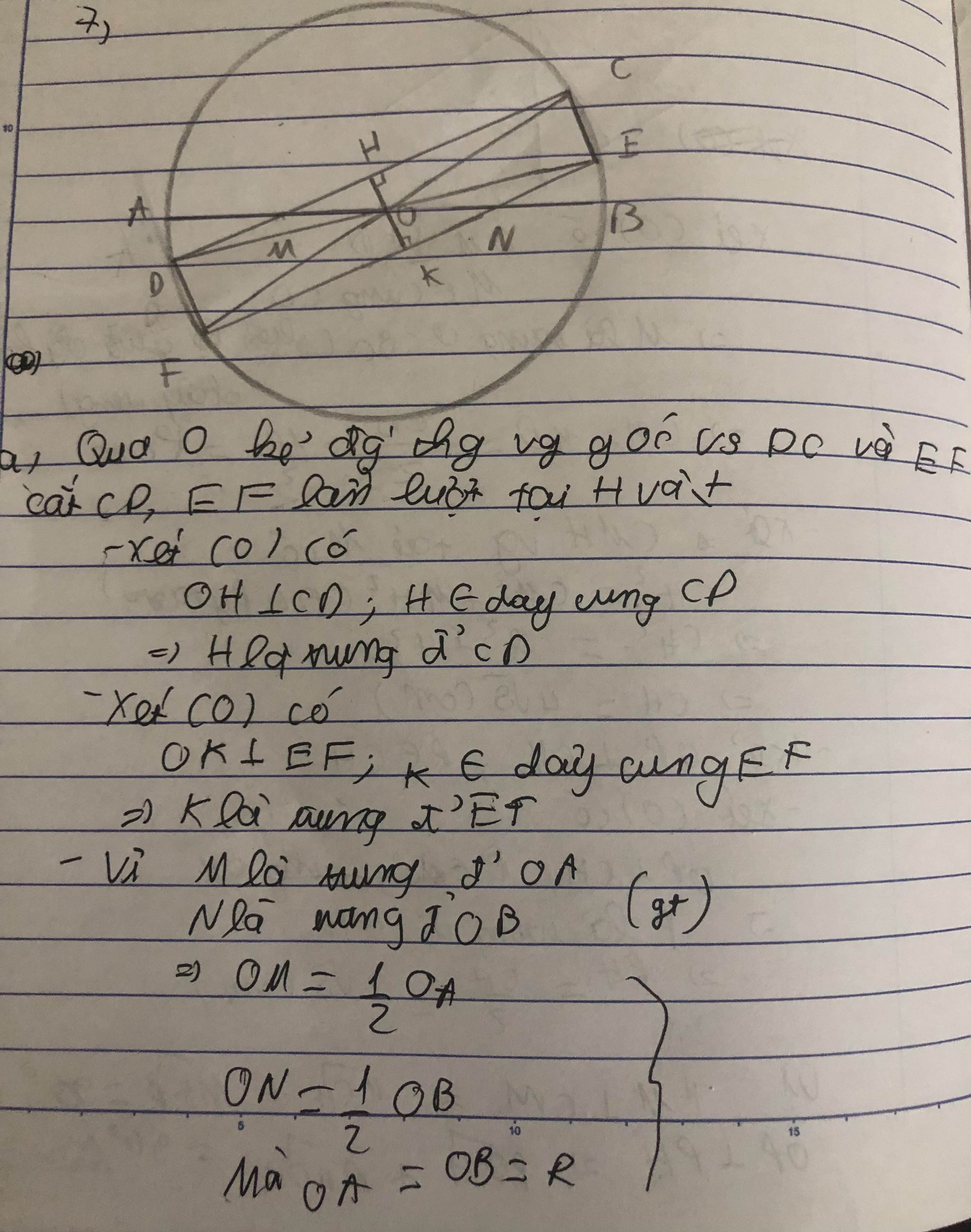Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GỌI H,K là chân đường vuông góc kẻ từ O xuống CD và EF.Sau đó chứng minh 3 điểm O,H,Kthẳng hàng.Xét 2 tam giác vuông MOH và NOK bằng nhau.=>CD=EF.=>CDEF là hình bình hành.(1)
Mặt khác ta có OH vuông góc với CD =>CH=MD=1/2CD
OK " " " EF=>KE=KF =1/2EF
=>HK là đường trung bình của hình bình hành CDEF.
=>HK//CE//DF MÀ HK vuông góc với EF =>CE vuông góc với EF.
=>GÓC CEF=90(2)
Từ (1),(2)=>CDEF là hình chữ nhật

a) qua O kẻ OPQ vuông góc với CD ; EF ( P thuộc CD; Q thuộc EF)
=> P C =PD ; QE =QF (1)
+ Mặt khác tam giác POM = QON ( cạnh huyền - góc nhọn)
=>OP =OQ
=> CD = EF (2)
(1)(2) => PC = QE mà PC//QE , P=Q =90 => PQCE là HCN
tương tự => PQFD là HCN
=> CDEF có 4 góc vuông là HCN
b)Xét tm giác POM vuông tại P có M =30
sin M = OP/OM => OP =OM.sin30 = R/2 . 1/2 = R/4
=> PQ = R/2 (3)
+ Tam giác POC uông tạ P => CP =\(\sqrt{R^2-\left(\frac{R}{4}\right)^2}=\frac{R\sqrt{15}}{4}\Rightarrow CD=\frac{R\sqrt{15}}{2}\)(4)
Từ (3)(4) => S =

Bài 2 nếu ai giải được thì làm ơn gửi cho mình cách giải nhé!!Mình cũng có bài này mà ko giải được