Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M A B O C
a, có AM = 2AC mà để AM lớn nhất
<=> AC lớn nhất
có AC là dây cung của đường tròn (O) đk AB
=> AC =< AB
dấu = xảy ra khi C trùng B
b, AM = 2R.căn 3 mà AM = 2AC
<=> 2AC = 2R.căn 3
<=> AC = R.căn 3
xét tam giác ABC vuông tại C => AC^2 + CB^2 = AB^2
Mà BA = 2R
=> (R.căn 3)^2 + BC^2 = (2R)^2
<=> 3R^2 + BC^2 = 4R^2
<=> BC^2 = R^2
<=> BC = R
vậy lấy điểm C trên (O) sao cho BC = R để AM = 2R.căn 3
c, xét tam giác BAM có BC là đường trung tuyến đồng thời là đường cao
=> tam giác BAM cân tại B
=> BA = BM mà AB không đổi
=> BM không đổi
=> khi C di động trên (O) thì M di động trên đường tròn (B) cố định

Theo quy tắc 4 điểm thì \(\hept{\begin{cases}OA+AB+O'B\ge OO'\\OA+OO'+O'B\ge AB\end{cases}}\Leftrightarrow\hept{\begin{cases}AB\ge OO'-\left(R+R'\right)\left(const\right)\\AB\le OO'+\left(R+R'\right)\left(const\right)\end{cases}}\)
=> AB nhỏ nhất khi A, B nằm giữa OO' ; A, B lớn nhất khi OO' nằm giữa AB

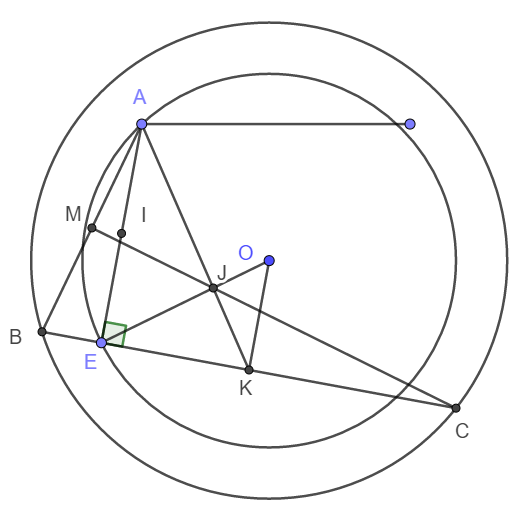
a) Gọi I, K lần lượt là trung điểm của AE và BC.
Ta có : \(EB^2=\left(BK-EK\right)^2;EC^2=\left(KC+EK\right)^2\)
\(\Rightarrow EB^2+EC^2=2\left(BK^2+EK^2\right)=2\left(BO^2-OK^2+OE^2-OK^2\right)\)
\(=2\left(R^2+r^2\right)-4OK^2\)
\(AE^2=4AI^2=4\left(r^2-OI^2\right)\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+6r^2-4\left(OI^2+OK^2\right)\)
Mà OIEK là hình chữ nhật nên \(OI^2+OK^2=OE^2=r^2\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+2r^2\) không đổi.
b) Giả sử EO giao với AK tại J.
Vì IOEK là hình chữ nhật nên OK song song và bằng EI. Vậy nên OK song song và bằng một nửa AE.
Do đó \(\frac{JE}{JO}=\frac{AJ}{JK}=\frac{AE}{OK}=2\)
Vì OE cố định nên J cố định; Vì AK là trung tuyến của tam giác ABC nên J là trọng tâm tam giác ABC
Suy ra J thuộc MC.
Vậy MC đi qua J cố định.
c) Vì AK = 3/2AJ nên H trùng K.
Do đó OH vuông góc BC. Suy ra H thuộc đường tròn đường kính OE.

O A M B C H K d
a) Ta có: MB và MC là 2 tiếp tuyến kẻ từ M tới đường tròn (O) => MB = MC và MO là phân giác ^BMC
Xét \(\Delta\)BCM cân tại M có đường phân giác MO => MO vuông góc BC tại H
=> ^OHK = 900 => \(\Delta\)OHK ~ \(\Delta\)OAM (g.g) => \(\frac{OH}{OA}=\frac{OK}{OM}\Rightarrow OA.OK=OH.OM\)
Xét \(\Delta\)MBO có ^MBO = 900 và BH vuông góc MO tại H
\(\Rightarrow OH.OM=OB^2=R^2\) (Hệ thức lượng trg tam giác vuông)
\(\Rightarrow OA.OK=R^2\) => OA.OK có giá trị ko đổi (đpcm).
\(\Leftrightarrow OK=\frac{R^2}{OA}\). Mà R2 và OA có độ dài ko đổi => OK có độ dài ko đổi.
Do K nằm trên OA cố định và OK ko đổi nên điểm K cố định.
=> BC luôn đi qua điểm K cố định (vì BC cắt OA tại K) (đpcm).
b) Ta thấy: ^OHK = 900 và OK không đổi (cmt)=> Điểm H di động trên 1 đường tròn cố đinh có đường kính OK.
c) Tứ giác MBOC có 2 đường chéo vuông góc với nhau nên \(S_{MBOC}=\frac{OM.BC}{2}\)
Ta có: \(OM\ge OA\)(Quan hệ đg xiên hình chiếu) \(\Rightarrow S_{MBOC}\ge\frac{OA.BC}{2}=R.BC\)(1)
Khi đó thì BC vuông góc OA => H trùng K => BC = 2.BK
Lại có: \(OK=\frac{R^2}{OA}=\frac{R^2}{2R}=\frac{R}{2}\). Áp dụng ĐL Pytago cho \(\Delta\)BKO:
\(\Rightarrow BK^2=OB^2-OK^2=R^2-\frac{R^2}{4}=\frac{3R^2}{4}\Leftrightarrow BK=\frac{\sqrt{3}.R}{2}\)
\(\Rightarrow BC=2.BK=\sqrt{3}.R\)(2)
Thế (2) vào (1) ta có: \(S_{MBOC}\ge\)\(\sqrt{3}.R.R=R^2\sqrt{3}\)
Vậy \(S_{MBOC}\)nhỏ nhất <=> Điểm M trùng với điểm A và \(Min_{S_{MBOC}}=R^2\sqrt{3}.\)
Bạn học trường THCS Ba Mỹ phải không?
Mình trường THCS Phú Ngãi?

a ta có \(\Delta\)OHK đồng dạng \(\Delta\)OAM \(\Rightarrow\)\(\frac{OK}{OM}\)=\(\frac{OH}{OA}\)\(\Rightarrow\)OK.OA=OH.OM
OM\(\perp\)BC\(\Leftrightarrow\)OC=OB NÊN O\(\in\)Đường trung trực của BC
MC=MB\(\Leftrightarrow\)M\(\in\)Đường trung trực của BC \(\Rightarrow\)OM\(\perp\)BC
XÉT \(\Delta\)OCM vuông tại C CH\(\perp\)OM\(\Rightarrow\)OC2=OH.OM \(\Rightarrow\)OK.OA ko đổi
a, tam giác 0HK đồng dạng với 0AM
0K/0M = 0H / 0A
nên 0K .0A = 0H.0M
em chúng minh 0M vuông góc với BC
0C = 0B nên 0 thuộc đường trung trực của BC
MC = MB nên M thuộc trung trực của BC
nên 0M là trung trực của BC
nên 0M vuông góc với BC tại H
tam giác 0CM vuông tại C , CH vuông góc với 0M
nên 0C^2 = 0H, 0M
nên không đổi nhé
Em chứng minh K không đổi đi
Theo câu a thầy chứng minh bên trên thì có:
OA.OK=OH.OM=OB^2=R^2
=>OA.OK=R^2=>OK=R^2/OA
Gọi I là trung điểm OK
tam giác OHK vuông tại H nên ta có:IH=1/2OK=R^2/2OA
mà O,A không đổi nên OA không đổi
=>IH không đổi
Hay H thuộc đường tròn tâm I bán kính R^2/2OA
với I là điểm nằm giữa O và A thỏa mãn OI=1/2OK=R^2/2OA
(đường tròn có tâm nằm trên đường thẳng OA và đi qua O bán kính R^2/2OA
Câu c em làm như sau nhé
Diện tích tứ giác MBOC=OM.HC
nên để diện tích tứ giác MBOC min thì OM.HC Min
Xét:OM^2.HC^2=OM^2.(OC^2-OH^2)=OM^2.OC^2-OM^2.OH^2=OM^2.R^2-R^4 (Do OM.OH=R^2)
=>Để OM,HC min thì OM^2.R^2 min hay OM^2 Min
mà OM>=OA (do OM là cạnh huyền của tam giác vuông OAM)
=>OM min <=>OM=OA hay M trùng với A
Khi đó OM^2.HC^2=(2R)^2.R^2-R^4=3R^4
=>Diện tích tứ giác MBOC Min=căn 3 R^2 <=>M trùng với A