Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc PAO+góc PMO=180 độ
=>PAOM nội tiếp
b: Xét (O) có
PA,PM là tiếp tuyến
=>PA=PM
mà OA=OM
nên OP là trung trực của AM
=>OP vuông góc AM
=>OP//MB

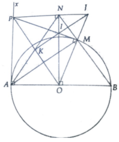
a, HS tự làm
b, Ta có OP ⊥ AM, BM ⊥ AM => BM//OP
c, chứng minh ∆AOP = ∆OBN => OP=BN
lại có BN//OP do đó OPNB là hình bình hành
d, Ta có ON ⊥ PI, PM ⊥ JO mà PM ∩ ON = I => I là trực tâm ∆POJ => JI ⊥ PO(1)
Chứng minh PAON hình chữ nhật => K trung điểm PO
Lại có A P O ^ = O P I ^ = I O P ^ => ∆IPO cân tại I => IKPO (2)
Từ (1),(2) => J,I,K thẳng hàng

1. Ta có ÐOMP = 900 ( vì PM ^ AB ); ÐONP = 900 (vì NP là tiếp tuyến ).
Như vậy M và N cùng nhìn OP dưới một góc bằng 900 => M và N cùng nằm trên đường tròn đường kính OP => Tứ giác OMNP nội tiếp.
2. Tứ giác OMNP nội tiếp => ÐOPM = Ð ONM (nội tiếp chắn cung OM)
Tam giác ONC cân tại O vì có ON = OC = R => ÐONC = ÐOCN
=> ÐOPM = ÐOCM.
Xét hai tam giác OMC và MOP ta có ÐMOC = ÐOMP = 900; ÐOPM = ÐOCM => ÐCMO = ÐPOM lại có MO là cạnh chung => DOMC = DMOP => OC = MP. (1)
Theo giả thiết Ta có CD ^ AB; PM ^ AB => CO//PM (2).
Từ (1) và (2) => Tứ giác CMPO là hình bình hành.
3. Xét hai tam giác OMC và NDC ta có ÐMOC = 900 ( gt CD ^ AB); ÐDNC = 900 (nội tiếp chắn nửa đường tròn ) => ÐMOC =ÐDNC = 900 lại có ÐC là góc chung => DOMC ~DNDC
=> => CM. CN = CO.CD mà CO = R; CD = 2R nên CO.CD = 2R2 không đổi => CM.CN =2R2không đổi hay tích CM. CN không phụ thuộc vào vị trí của điểm M.
.