Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

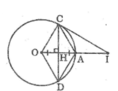
a) Gọi H là giao điểm của OA và CD
Vì CD là đường trung trực của OA nên:
CD ⊥ OA và HA = HO
Mà CD ⊥ OA nên HC = HD (đường kính dây cung)
Vì tứ giác ACOD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.
Đồng thời CD ⊥ OA nên ACOD là hình thoi.
b) Vì ACOD là hình thoi nên AC = OC
Mà OC = OA ( = R) nên tam giác OAC đều
Suy ra: ^COA=60∘COA^=60∘ hay ˆCOI=60∘
Mà CI ⊥ OC (tính chất tiếp tuyến)
Trong tam giác vuông OCI, ta có:
CI=OC.tgˆCOI=R.tg60∘=R√3CI=OC.tgCOI^=R.tg60∘=R3.

Vì ACOD là hình thoi nên AC = OC
Mà OC = OA (= R) nên tam giác OAC đều


O I A B C D M
a/ Ta có AB vuông góc với DC => IC =ID
Tam giác CMD cân tại M và I là trung điểm của DC nên MI vuông góc với DC
Từ hai cái trên ta kết luận M,A,B thẳng hàng
b/ Theo đề bài và câu a ta có
CI = ID
AI = IO
=> Tứ giác OCAD là hình bình hành
ta lại có AO vuông góc với CD
=> Tứ giác OCAD là hình thoi
