Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

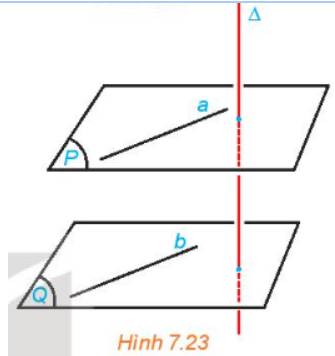
\(\left. \begin{array}{l}\Delta \bot \left( P \right)\\a \subset \left( P \right)\end{array} \right\} \Rightarrow \Delta \bot a,a//b \Rightarrow \Delta \bot b \Rightarrow \left( {\Delta ,b} \right) = {90^0}\)
\(\Delta \bot a \Rightarrow \left( {\Delta ,a} \right) = {90^0}\)
\( \Rightarrow \) (\(\Delta \), b) = (\(\Delta \), a) mà b là đường thẳng bất kì thuộc (Q)
\( \Rightarrow \) \(\Delta \bot \left( Q \right)\)

a: \(\text{Δ}\perp a\)
a//a'
=>Δ vuông góc a'
mà Δ vuông góc (P)
nên a'//(P) hoặc \(a'\subset\left(P\right)\)
mà \(a'\cap\left(P\right)=\left\{O\right\}\)
nên a' nằm trong (P)
b: a'//a
\(a'\subset\left(P\right)\)
=>a//(P) hoặc \(a\subset\left(P\right)\)

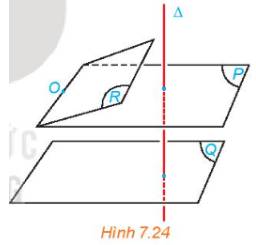
a) (R) // (Q); \(\Delta \) \( \bot \) (Q) \( \Rightarrow \) \(\Delta \) \( \bot \) (R)
Mà \(\Delta \) \( \bot \) (P) và (R), (Q) là 2 mặt phẳng cùng đi qua O
\( \Rightarrow \) (R) trùng (P)
b) (R) // (Q) mà (R) trùng (P) nên (P) // (Q)

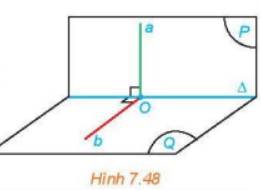
a) \(\left. \begin{array}{l}\left( P \right) \cap \left( Q \right) = \Delta \\\left( P \right):a \bot \Delta \\\left( Q \right):b \bot \Delta \end{array} \right\} \Rightarrow \left( {\left( P \right),\left( Q \right)} \right) = \left( {a,b} \right)\)
Mà \(\left( P \right) \bot \left( Q \right) \Rightarrow \left( {\left( P \right),\left( Q \right)} \right) = {90^0} \Rightarrow \left( {a,b} \right) = {90^0}\)
b) \(\left( {a,b} \right) = {90^0} \Rightarrow a \bot b,a \bot \Delta ,b \cap \Delta \Rightarrow a \bot \left( Q \right)\)

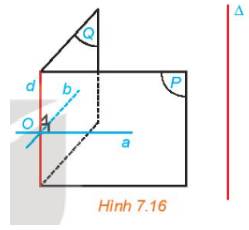
\(\left. \begin{array}{l}a \bot d\\d//\Delta \end{array} \right\} \Rightarrow \Delta \bot a\)
\(\left. \begin{array}{l}b \bot d\\d//\Delta \end{array} \right\} \Rightarrow \Delta \bot b\)
Mà \(a \cap b = \left\{ O \right\}\) \( \Rightarrow \) mp(a, b) đi qua O và vuông góc với \(\Delta \).

a) Đúng
b) Đúng
c) Sai (vì a có thể nằm trong mp(α), xem hình vẽ)
d) Sai, chẳng hạn hai mặt phẳng (α) và (β) cùng đi qua đường thẳng a và a ⊥ mp(P) nên (α) và (β) cùng vuông góc với mp(P) nhưng (α) và (β) cắt nhau.
e) Sai, chẳng hạn a và b cùng ở trong mp(P) và mp(P) ⊥ d. Lúc đó a và b cùng vuông góc với d nhưng a và b có thể không song song nhau.

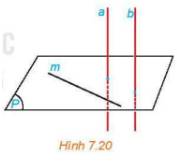
\(\left. \begin{array}{l}a \bot \left( P \right)\\m \subset \left( P \right)\end{array} \right\} \Rightarrow a \bot m \Rightarrow \left( {a,m} \right) = {90^0}\)
a // b \( \Rightarrow \left( {a,m} \right) = \left( {b,m} \right) = {90^0}\) mà đường thẳng m bất kì thuộc mặt phẳng (P)
\( \Rightarrow \) b \( \bot \) (P).
Vì a // (P) nên a // b sao cho b \( \subset \) (P)
\( \Rightarrow \) (\(\Delta \); a) = (\(\Delta \); b)
Mà \(\Delta \) \( \bot \) (P); b \( \subset \) (P) nên \(\Delta \) \( \bot \) b \( \Rightarrow \) (\(\Delta \); b) = 900
Vậy (\(\Delta \); a) = 900