Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)

Bài 3:
Gọi M là giao điểm \(d_1;d_2\Rightarrow\) tọa độ M là nghiệm:
\(\left\{{}\begin{matrix}x+y-1=0\\x-3y+3=0\end{matrix}\right.\) \(\Rightarrow M\left(0;1\right)\)
Gọi \(A\left(1;0\right)\) là 1 điểm thuộc \(d_1\)
\(d_3\) đối xứng \(d_2\) qua \(d_1\Leftrightarrow d_1\) là phân giác góc tạo bởi \(d_2;d_3\)
\(\Rightarrow d_3\) qua M và \(d\left(A;d_3\right)=d\left(A;d_2\right)\)
Gọi pt \(d_3\) có dạng \(a\left(x-0\right)+b\left(y-1\right)=0\Leftrightarrow ax+by-b=0\)
Theo công thức khoảng cách:
\(\frac{\left|a.1+b.0-b\right|}{\sqrt{a^2+b^2}}=\frac{\left|1-3.0+3\right|}{\sqrt{1+3^2}}\Leftrightarrow\frac{\left|a-b\right|}{\sqrt{a^2+b^2}}=\frac{\sqrt{8}}{\sqrt{5}}\)
\(\Leftrightarrow5\left(a-b\right)^2=8\left(a^2+b^2\right)=3a^2+10ab+3b^2=0\)
\(\Leftrightarrow\left(a+3b\right)\left(3a+b\right)=0\Rightarrow\left[{}\begin{matrix}a=-3b\\b=-3a\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn:
\(\left[{}\begin{matrix}-3bx+by-b=0\\ax-3ay+3a=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}3x-y+1=0\\x-3y+3=0\end{matrix}\right.\)
Bài 2:
a/ Gọi d' là đường thẳng qua M và vuông góc d
\(\Rightarrow d'\) nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình d':
\(2\left(x-2\right)-1\left(y-5\right)=0\Leftrightarrow2x-y+1=0\)
H là giao điểm của d và d' nên tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x+2y-2=0\\2x-y+1=0\end{matrix}\right.\) \(\Rightarrow H\left(0;1\right)\)
b/ M' đối xứng M qua d \(\Leftrightarrow H\) là trung điểm \(MM'\)
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M\\y_{M'}=2y_H-y_M\end{matrix}\right.\) \(\Rightarrow M'\left(-2;-3\right)\)
c/ d' đối xứng d qua M \(\Rightarrow\) phương trình d' có dạng: \(x+2y+c=0\) với \(c\ne-2\)
Ta có: \(d\left(M;d\right)=d\left(M;d'\right)\)
\(\Leftrightarrow\frac{\left|2+2.5-2\right|}{\sqrt{1^2+2^2}}=\frac{\left|2+2.5+c\right|}{\sqrt{1^2+2^2}}\)
\(\Rightarrow\left|c+12\right|=10\Rightarrow\left[{}\begin{matrix}c=-2\left(l\right)\\c=-22\end{matrix}\right.\)
Phương trình d': \(x+2y-22=0\)

A B C M G N B1
a, Gọi N là trung điểm của AC
Ta có \(\overrightarrow{CB_1}=\overrightarrow{CB}+\overrightarrow{BB_1}\)
\(=\overrightarrow{CA}+\overrightarrow{AB}+\frac{4}{3}\overrightarrow{BN}\) ( vì \(\left\{{}\begin{matrix}BB_1=2BG\\BG=\frac{2}{3}BN\end{matrix}\right.\) )
\(=\overrightarrow{CA}+\overrightarrow{AB}+\frac{4}{6}\left(\overrightarrow{BA}+\overrightarrow{BC}\right)\)
\(=\overrightarrow{CA}+\overrightarrow{AB}+\frac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\left(\overrightarrow{CA}+\frac{2}{3}\overrightarrow{AC}\right)+\left(\overrightarrow{AB}+\frac{4}{3}\overrightarrow{BA}\right)\)
\(=\frac{-1}{3}\left(\overrightarrow{AB}+\overrightarrow{ÂC}\right)\)
b, \(\overrightarrow{AB_1}=\overrightarrow{AB}+\overrightarrow{BB_1}\) rồi tương tự câu a nha bạn
c, \(\overrightarrow{MB_1}=\overrightarrow{MB}+\overrightarrow{BB_1}=\frac{1}{2}\overrightarrow{CB}+\overrightarrow{BB_1}\)

Hoang Duong chắc tag ko dính :< Có phải là delta vuông góc với (d) đúng ko? Đó, vậy nên vecto chỉ phương của delta sẽ là vecto pháp tuyến của (d). Mà vecto pháp tuyến của delta là (2;-3) nên vecto chỉ phương của delta sẽ là (3;2)
\n\nChung quy lại, nói một cách ngắn gọn và dễ hiểu: nếu 2 đường thẳng vuông góc với nhau thì vecto chỉ phương của đường thẳng này sẽ là vecto pháp tuyến của đường thẳng kia và ngược lại :)
\n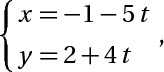 d2:
d2: 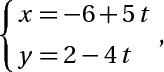
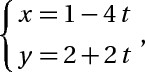 d2 : 2x+4y-10=0
d2 : 2x+4y-10=0