Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)
a.Xét tam giác ABC và tam giác HBA, có:
^B: chung
^BAC = ^BHA = 90 độ
Vậy tam giác ABC đồng dạng tam giác HBA (g.g)
b.\(\rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
\(\Leftrightarrow AB^2=BH.BC\left(đfcm\right)\) (1)
c.Áp dụng định lý pitago \(\Rightarrow BC=\sqrt{6^2+10^2}=2\sqrt{34}\left(cm\right)\)
(1) \(\Leftrightarrow6^2=2\sqrt{34}BH\)
\(\Leftrightarrow BH=\dfrac{9\sqrt{34}}{17}\left(cm\right)\)
Áp dụng định lý pitago trong tam giác ABH \(\Rightarrow AH=\sqrt{6^2-\left(\dfrac{9\sqrt{34}}{17}\right)^2}=\dfrac{15\sqrt{34}}{17}\left(cm\right)\)

a.
Xét hai tam giác vuông HBA và ABC có:
\(\left\{{}\begin{matrix}\widehat{HBA}\text{ chung}\\\widehat{AHB}=\widehat{BAC}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta HBA\sim\Delta ABC\left(g.g\right)\)
b.
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Do \(\Delta HBA\sim\Delta ABC\left(cmt\right)\Rightarrow\dfrac{AH}{AC}=\dfrac{AB}{BC}\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
Áp dụng định lý Pitago trong tam giác vuông HBA:
\(BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=3,6\left(cm\right)\)

a) Xét ΔHBA và ΔABC có:
^A=^H=90o
^HAB=^ACB(cùng phụ với ^ABC)
→ ΔHBA∼ΔABC(g.g)
b) Áp dụng định lí Pytago vào tam giác vuông ABC, ta có:
\(BC=\sqrt{20^2+15^2}=25cm\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AB.AC\)
\(\rightarrow AH.BC=AB.AC\)
\(\rightarrow AH=\dfrac{AB.AC}{BC}=12cm\)
c) Xét ΔAHB và ΔCHA có:
^AHB=^CHA=90o
^HCA=^HAB(cùng phụ với ^ABC)
→ ΔAHB∼ΔCHA(g.g)
\(\rightarrow\dfrac{AH}{HB}=\dfrac{HC}{AH}\left(tươngứng\right)\)
\(\rightarrow AH^2=HB.HC\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó:ΔABC\(\sim\)ΔHBA
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\)
Do đó:ΔHBA\(\sim\)ΔHAC
c: \(BH=\sqrt{15^2-12^2}=9\left(cm\right)\)
\(BC=\dfrac{AB^2}{BH}=\dfrac{15^2}{9}=25\left(cm\right)\)
\(AC=\sqrt{25^2-15^2}=20\left(cm\right)\)
d: ta có: ΔHBA\(\sim\)ΔHAC
nên HB/HA=HA/HC
hay \(HA^2=HB\cdot HC\)

A B C H I 3 5 K M N
a) Xét \(\Delta ABC\)và \(\Delta HBA\)có
\(\widehat{A}=\widehat{H}=90^o\)
\(\widehat{B}\)là góc chung
\(\Rightarrow\Delta ABC~\Delta HBA\left(g.g\right)\)
\(\Leftrightarrow\frac{AB}{BH}=\frac{AC}{AH}\Leftrightarrow AB.AH=BH.AC\left(đpcm\right)\)
b) Xét \(\Delta HBA\)vuông tại H theo định lý PYTAGO ta co
\(\Rightarrow HA=\sqrt{AB^2-BH^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
Vì BI là phân giác của góc ABH
\(\Rightarrow\frac{AI}{AB}=\frac{IH}{BH}\Leftrightarrow\frac{AI}{5}=\frac{IH}{3}\)và AI + IH = HA = 4
Theo tính chất dãy tỉ số bằng nhau ta có
\(\frac{AI}{5}=\frac{IH}{3}=\frac{AI+IH}{5+3}=\frac{4}{8}=\frac{1}{2}\)
\(\Rightarrow\hept{\begin{cases}\frac{AI}{5}=\frac{1}{2}\Leftrightarrow AI=\frac{5.1}{2}=2,5\left(cm\right)\\\frac{IH}{3}=\frac{1}{2}\Leftrightarrow IH=\frac{3.1}{2}=1,5\left(cm\right)\end{cases}}\)
c) Xét tam giác CHA và tam giác AHB
\(\widehat{H}=\widehat{H}=90^o\)
\(\widehat{A}=\widehat{B}\)( cùng phụ góc C)
=> Tam giác CHA ~ tam giác AHB (gg)
\(\Rightarrow\frac{AC}{AB}=\frac{AH}{HB}\Leftrightarrow\frac{AC}{AH}=\frac{AB}{HB}\)(*)
Vì BI là phân giác của tam giác AHB
\(\Leftrightarrow\frac{AI}{AH}=\frac{AB}{BH}\left(1\right)\)
Vì CK là phân giác của tam giác AHC
\(\Leftrightarrow\frac{CK}{KH}=\frac{AC}{AH}\left(2\right)\)
Từ (1), (2) và (*)
\(\Rightarrow\frac{AI}{AH}=\frac{CK}{KH}\Leftrightarrow KI//AC\left(taletdao\right)\)
d) Gọi N là giao điểm của HM và AC
=> bài toán trở thành chứng minh N là trung điểm
bạn ơi đề cho N là trung điểm rồi mà sao phải chứng minh

a, Xét ΔABC và ΔHBA có:
∠BAC chung, ∠BHA=∠BAC (=90o)
=> ΔABC ∼ ΔHBA (g.g)
b, Áp dụng đ/l Pitago vào △ABC ta có:
BC2=AB2+AC2 => BC=√(62+82)=10 (cm)
Ta có: SABC=\(\dfrac{1}{2}\)AB.AC=\(\dfrac{1}{2}\)AH.BC
=> 6.8=AH.10 => AH=4,8 (cm)
c, Xét △HAB và △HCA có:
∠BHA=∠CHA (=90o), ∠ABC=∠HAC (cùng phụ ∠BCA)
=> △HAB ∼ △HCA (g.g)
=> \(\dfrac{AB}{AC}=\dfrac{\text{△HAB}}{\text{△HCA}}\)=\(\dfrac{6}{8}\)=\(\dfrac{3}{4}\)
d, AD là đường p/g của △ABC => \(\dfrac{AB}{BD}=\dfrac{AC}{DC}\)=\(\dfrac{AB+AC}{BD+DC}=\dfrac{14}{10}=\dfrac{7}{5}\)
=> \(\dfrac{AB}{BD}=\dfrac{7}{5}\) => \(\dfrac{6}{BD}=\dfrac{7}{5}\) => BD=\(\dfrac{30}{7}\) (cm)
=> \(\dfrac{AC}{DC}\)\(=\dfrac{7}{5}\) => \(\dfrac{8}{DC}=\dfrac{7}{5}\) => DC=\(\dfrac{40}{7}\) (cm)

A B C H
a)Xét tam giác HAB và tam giác ABC
góc ABC : chung
góc BHA=góc BAC=90o
Suy ra: tam giác HAB ~ tam giác ABC (g-g)
b)Ta có: tam giác ABC vuông tại A
=>AC2=BC.HC (hệ thức lượng)
c)Ta có: \(BC^2=AB^2+AC^2=15^2+20^2=625\Rightarrow BC=25\left(cm\right)\)
Ta lại có: \(AC^2=BC.HC\left(HTL\right)\Rightarrow HC=\frac{AC^2}{BC}=\frac{20^2}{25}=16\left(cm\right)\)

a) Xét ΔHBA và ΔABC có:
∠BHA = ∠BAC = 900 ( GT)
Góc B: Chung
Vậy ΔHBA ~ ΔABC (g.g)
b) Xét ΔHAC và ΔABC.có:
∠AHC = ∠BAC =900 ( GT)
Góc C : Chung
Vậy ΔHAC ~ ΔABC (g.g)
Suy ra:
![]()
c) Áp dụng định lí Pytago cho vuông tại A, ta có:
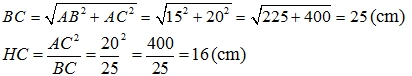

Lời giải:
a. Xét tam giác $HBA$ và $ABC$ có:
$\widehat{B}$ chung
$\widehat{BHA}=\widehat{BAC}=90^0$
$\Rightarrow \triangle HBA\sim \triangle ABC$ (g.g)
b. Từ tam giác đồng dạng phần a suy ra:
$\frac{HB}{BA}=\frac{AB}{BC}$
$\Rightarrow AB^2=BH.BC=3,6.10=36$
$\Rightarrow AB=6$ (cm)
$AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=8$ (cm) theo định lý Pitago
Hình vẽ: