Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi H1, H2, H3 lần lượt là trực tâm ΔABC1, ΔBCA1, ΔCAB1
Ta có : \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC_1}=\overrightarrow{OH}_1\left(1\right)\)
\(\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OA}_1=\overrightarrow{OH}_2\left(2\right)\)
\(\overrightarrow{OC}+\overrightarrow{OA}+\overrightarrow{OB}_1=\overrightarrow{OH}_3\left(3\right)\)
Trừ theo vế (1) , (2) ta có :
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC'}+\overrightarrow{BO}+\overrightarrow{CO}+\overrightarrow{A_1O}=\overrightarrow{OH_1}+\overrightarrow{H_2O}\)
\(\Leftrightarrow\overrightarrow{A_1A}+\overrightarrow{CC_1}=\overrightarrow{H_2H_1}\)
TƯƠNG TỰ TRỪ THEO VẾ (2) , (3) ta được :
\(\overrightarrow{B_1B}+\overrightarrow{A_1A}=\overrightarrow{H_3H_2}\)
Lại có: AA1//BB1//CC1 (gt)
\(\Rightarrow\)vt AA1, vtA1A, vt B1B, CC1 cùng phương
\(\RightarrowĐPCM\)

lời giải hơi ngắn
Áp dụng định lí pascal biến thể cho bộ 6 ( A , B , C , A , B , C ) với AA giao BC tại A1 , BB giao AC tại B , CC giao BC tại C1 ( với AA , BB ,CC lần lượt là các tiếp tuyến tại A , B ,C ) ta có A1 , B1 , C1 thẳng hàng

1) d cắt trục hoành tại điểm A(1:0)=>0=a*1+b (1)
d// vs đường thẳng y=-2+2003=> a=-2 và b\(\ne\)2003 (2)
từ (1) và (2)=>\(\left\{{}\begin{matrix}a=-2\\b=2\left(\ne2003\right)\end{matrix}\right.\)
Vậy d:y=-2x+2
Bài 2:
1: Tọa độ A là: 2x+2=-x+2 và y=2x+2
=>x=0 và y=2
Tọa độ B là: y=0 và 2x+2=0
=>x=-1 và y=0
Tọa độ C là:
y=0 và 2-x=0
=>C(2;0)
2: Để (d3) cắt cả (d1) và (d2) thì \(\left\{{}\begin{matrix}m< >2\\m< >-1\end{matrix}\right.\Leftrightarrow m\notin\left\{2;-1\right\}\)

Nếu tam giác ABC và A1B1C1 có cùng trọng tâm G thì \(\overrightarrow{AA_1}+\overrightarrow{BB_1}+\overrightarrow{CC_1}=\overrightarrow{0}\) bạn biết cái này chưa ?

Bài 1:
H1;H2 lần lượt là trực tâm tam giác OAB, OCD và \(\widehat{AOB}=\widehat{COD}\)(đối đỉnh)
=> \(\frac{OH_1}{OH_2}=\frac{AB}{CD}\)
Gọi M,N,K lần lượt là trung điểm của các đoạn thẳng AD, BC, BD
Vì G1;G2 lần lượt là trọng tâm của các tam giác OAD; OBC. Nên \(\frac{OG_1}{OM}=\frac{2}{3};\frac{OG_2}{ON}=\frac{2}{3}\)
\(\Delta\)OMN có: \(\frac{OG_1}{OM}=\frac{OG_2}{ON}\left(=\frac{2}{3}\right)\)=> G1G2 // MN và \(G_1G_2=\frac{2}{3}MN\)
\(OH_1\perp MK,OH_2\perp NK,MK=\frac{AB}{2},NK=\frac{CD}{2}\)
Do đó: \(\widehat{H_1OH_2}=\widehat{MKN},\frac{OH_1}{MK}=\frac{OH_2}{NK}\). Nên \(\Delta\)OH1H2 đồng dạng với \(\Delta\)KMN (cgc)
=> \(H_1H_2\perp MN\)Mà G1G2 // MN
Nên \(H_1H_2\perp G_1G_2\)=> \(S=\frac{1}{2}H_1H_2\cdot G_1G_2\)
Áp dụng BĐT Cosi cho 2 số dương ta có:
\(S=\frac{1}{2}H_1H_2\cdot G_1G_2=\frac{3G_1G_2\cdot H_1H_2}{6}\le\frac{\left(3G_1G_2+H_1H_2\right)^2}{24}\)
Dấu "=" <=> \(3G_1G_2=H_1H_2\Leftrightarrow OH_1=AB\)và \(OH_2=CD\)
\(\Leftrightarrow\widehat{AOB}=\widehat{COD}=45^o\)
Bài 2: *có nhiều cách làm bài này, mỗi cách có 1 hình khác nhau, đang lỗi nên không vẽ được hình*
Cách 1: Ta có: \(\widehat{BAC}=90^o\)(Góc nội tiếp chắn nửa đường tròn)
Đặt BH=x, ta có HC=HB-BH=2R-x
\(\Delta\)ABC vuông tại A, AH là đường cao
=> AH2=BH.HC. Nên \(AH=\sqrt{x\left(2R-x\right)}\)
Áp dụng BĐT Cosi cho 2 số dương, ta có: AH+BH=\(\sqrt{x\left(2R-x\right)+x}=\frac{1}{\sqrt{3+2\sqrt{2}}}\sqrt{x\left[\left(3+2\sqrt{2}\right)\left(2R-x\right)\right]}+x\)
\(\le\frac{1}{\sqrt{\left(\sqrt{2}+1\right)^2}}\cdot\frac{a+\left(3+2\sqrt{2}\right)\left(2R-x\right)}{2}+x\)\(=\frac{1}{\sqrt{2}+1}\left[\frac{x}{2}\left(\sqrt{2}+1\right)^2\cdot R-\frac{\left(\sqrt{2}+1\right)^2\cdot x}{2}\right]+x\)
\(=\frac{\sqrt{2}-1}{2}\cdot x+\left(\sqrt{2}+1\right)R-\frac{\sqrt{2}+1}{2}x+x=\left(\sqrt{2}+1\right)R\)
Ta có AB+AH \(\le\left(\sqrt{2}+1\right)R\)không đổi
Dấu "=" xảy ra <=> \(x=\left(3+2\sqrt{2}\right)\left(2R-x\right)\)
\(\Leftrightarrow x=\frac{2+\sqrt{2}}{2}R\)
\(\Leftrightarrow\widehat{AOC}=45^o\)
Cách 2: Gọi M là điểm trên nửa đường tròn (O) sao cho \(\widehat{COM}=45^o\) và gọi N là giao của nửa đường tròn (O) tại M với BC
Ta có: M,N cố định; \(\widehat{ONM}=45^o\), BN không đổi
Điểm A trên đường tròn (O)
Do đó tia NA nằm giữa 2 tia NB và NM
\(\Rightarrow\widehat{ANH}\le\widehat{ONM}=45^o\). Mà \(\widehat{ANH}+\widehat{HAN}=90^o\), Nên \(\widehat{HAN}\ge45^o\)
=> \(\widehat{ANH}\le\widehat{HAN},\)\(\Delta\)AHN có: \(\widehat{ANH}\le\widehat{HAN}\Rightarrow AH\le HN\)
Do đó: AH+BH \(\le\)HN+BH=BN, không đổi
Dấu "=" xảy ra <=> A = M
Vậy khi A trên nửa đường tròn (O) sao cho \(\widehat{COA}=45^o\) thì AH+BH lớn nhất

A B C E F P D G (O ) (O ) 1 2
Gọi hai tiếp tuyến tại E và F của (AEF) cắt nhau tại G. Áp dụng ĐL Pascal ta có ngay B,G,C thẳng hàng (1)
Ta thấy PG/(O1) = GE2 = PG/(AEF) = GF2 = PG/(O2) suy ra G nằm trên trục đẳng phương của (O1) và (O2) (2)
Ta lại có (O1) cắt (O2) tại D; D,B,C thẳng hàng. Kết hợp với (1) và (2) ta thu được BC là trục đẳng phương của (O1) và (O2) (đpcm).
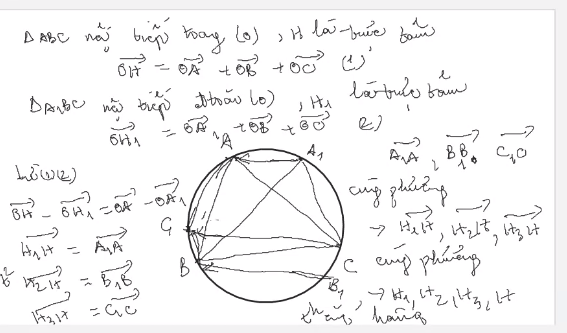
Gọi H1, H2, H3 lần lượt là trực tâm ΔABC1, ΔBCA1, ΔCAB1
Ta có: \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}_1=\overrightarrow{OH_1}\)(1)
\(\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OA_1}=\overrightarrow{OH_2}\)(2)
\(\overrightarrow{OC}+\overrightarrow{OA}+\overrightarrow{OB_1}=\overrightarrow{OH_3}\) (3)
Trừ theo vế (1), (2) ta có:
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC'}+\overrightarrow{BO}+\overrightarrow{CO}+\overrightarrow{A_1O}=\overrightarrow{OH_1}+\overrightarrow{H_2O}\)
\(\Leftrightarrow\overrightarrow{A_1A}+\overrightarrow{CC_1}=\overrightarrow{H_2H_1}\)
trương tự trừ theo vế (2), (3) ta được:
\(\overrightarrow{B_1B}+\overrightarrow{AA_1}=\overrightarrow{H_3H_2}\)
Lại có: AA1//BB1//CC1 (gt)
=> vt AA1, vtA1A, vt B1B, CC1 cùng phương
=> đpcm
@Nguyễn Việt Lâm