TH
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
T
1
31 tháng 8 2017
kẽ đường cao AH,tam giác ABC cân tại A=>AH cũng là trung tuyến của BC=>BH=1/2BC=5cm
xét tam giác AHB theo DL Pitago ta tính dc AH=12cm
=>cosBAH=AH/AB=12/13
=>cosBAC=2*12/13=24/13(vì AH là fân giác góc BAC)
CM
22 tháng 7 2017
Vì tam giác ABC cân tại A nên AE là đường cao đồng thời là đường trung tuyến
=> E là trung điểm BC => EB = EC = 5
Xét ABE vuông tại E có:
Mặt khác:
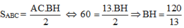
Xét ABH vuông tại H có:
Đáp án cần chọn là: A
3 tháng 9 2021
Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay AC=12(cm)
Xét ΔACB vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}CH=\dfrac{144}{13}\left(cm\right)\\AH=\dfrac{60}{13}\left(cm\right)\end{matrix}\right.\)
DH
1
26 tháng 8 2023
Gọi O là tâm đường tròn ngoại tiếp ΔABC
Gọi H là giao của AO với BC
AB=AC
OB=OC
Do đó: AO là trung trực của BC
=>AH là trung trực của BC
=>H là trung điểm của BC
HB=HC=4/2=2cm
Kẻ giao của AO với (O) là D
=>AD là đường kính của (O)
Xét (O) có
ΔABD nội tiếp
ADlà đường kính
Do đó: ΔBAD vuông tại B
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>\(AH^2=6^2-2^2=32\)
=>\(AH=4\sqrt{2}\left(cm\right)\)
Xét ΔBAD vuông tại B có BH là đường cao
nên AB^2=AH*AD
=>\(AD=\dfrac{6^2}{4\sqrt{2}}=\dfrac{9}{\sqrt{2}}\left(cm\right)\)
=>\(R=\dfrac{AD}{2}=\dfrac{9}{2\sqrt{2}}\left(cm\right)\)
2 tháng 10 2021
Bài 2:
b: \(AH\cdot\left(\cot\widehat{B}+\cot\widehat{C}\right)\)
\(=AH\cdot\left(\dfrac{BH}{AH}+\dfrac{CH}{AH}\right)\)
\(=AH\cdot\dfrac{BC}{AH}=BC\)
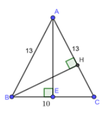
A B C H K Từ A kẻ đường cao AH vuông góc với BC tại H.
Từ B kẻ đường cao BK vuông góc với AC tại K
Khi đó, ta có BH = HC = 1/2BC = 5 (cm)
\(AH=\sqrt{AC^2-\left(\frac{BC}{2}\right)^2}=13^2-5^2=12\left(cm\right)\)
Dễ thấy hai tam giác HCA và KCB đồng dạng (g.g)
Suy ra \(\frac{HC}{KC}=\frac{AC}{BC}\) hay \(\frac{5}{KC}=\frac{13}{10}\Rightarrow KC=\frac{50}{13}\Rightarrow AK=AC-KC=13-\frac{50}{13}=\frac{119}{13}\left(cm\right)\)
Xét tam giác AKB, ta có :
\(CosA=\frac{AK}{AC}=\frac{\frac{119}{13}}{13}=\frac{119}{169}\)
kẽ đường cao AH,tam giác ABC cân tại A=>AH cũng là trung tuyến của BC=>BH=1/2BC=5cm
xét tam giác AHB theo DL Pitago ta tính dc AH=12cm
=>cosBAH=AH/AB=12/13
=>cosBAC=2*12/13=24/13(vì AH là fân giác góc BAC)