Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
b: \(\dfrac{3}{2}< >\dfrac{2}{-3}\)
nên hệ có 1 nghiệm duy nhất
c: 3/2<>0/1
nên hệ có 1 nghiệmduy nhất
d: 0/1<>-1/-1
nên hệ có 1 nghiệm duy nhất
e: 1/2=2/4<>3/1
nên hệ ko có nghiệm
f: 1:1/2=1:1/2=1:1/2
nên hệ có vô số nghiệm
Còn lại tương tự
Bài 5:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x-y=5\\2x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=1+2y=3\end{matrix}\right.\)
c; THay x=3 và y=1 vào (d3), ta được:
3m+1(2m-1)=3
=>5m-1=3
=>5m=4
=>m=4/5
a,
\(\left\{{}\begin{matrix}2x+y=1\\x-y=2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}2x+y+x-y=1+2\\x-y=2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}3x=3\\x-y=2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=1\\1-y=2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
b, không có nghiệm.
c, không giải được.
a: =>3x=3 và x-y=2
=>x=1 và y=-1
b: =>0x=-3 và x+2y=2
=>Hệ vô nghiệm
c: =>2x+y=3 và 2x+y=3
=>0x=0 và 2x+y=3
=>Hệ có vô số nghiệm theo dạng tổng quát là \(\left\{{}\begin{matrix}x\in R\\y=3-2x\end{matrix}\right.\)
Giải hệ sau :
Câu a :
\(\left\{{}\begin{matrix}x+y=-1\\2x+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=-1\\-x=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=-1\\x=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)
Vậy ...........................
Câu b :
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=a\\\dfrac{1}{y}=b\end{matrix}\right.\) . Ta có :
\(\left\{{}\begin{matrix}a+b=\dfrac{1}{5}\\3a+4b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+3b=\dfrac{3}{5}\\3a+4b=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-b=-\dfrac{7}{5}\\3a+4b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{7}{5}\\a=-\dfrac{6}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{7}{5}\\\dfrac{1}{y}=-\dfrac{6}{5}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{7}\\y=-\dfrac{5}{6}\end{matrix}\right.\)
Vậy..................
\(a,\left\{{}\begin{matrix}2x-y=4\\x+5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y=4\\2x+10y=6\end{matrix}\right.\left\{{}\begin{matrix}11y=2\\2x+10y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2}{11}\\2x+10.\dfrac{2}{11}=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2}{11}\\2x=\dfrac{46}{11}\end{matrix}\right.\left\{{}\begin{matrix}y=\dfrac{2}{11}\\x=\dfrac{23}{11}\end{matrix}\right.\)
\(1,\Leftrightarrow\left\{{}\begin{matrix}x=2y+4\\-4y-8+5y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\cdot5+4=14\\y=5\end{matrix}\right.\\ 2,\Leftrightarrow\left\{{}\begin{matrix}5x-30+6x=3\\y=10-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\\ 3,\Leftrightarrow\left\{{}\begin{matrix}x=4-2y\\6y-12+y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{10}{7}\\y=\dfrac{19}{7}\end{matrix}\right.\)
a) ⇔
⇔
Ta có:
a = a' = 1, b = b' = - .
=> Hai đường thẳng trùng nhau.
Vậy hệ phương trình có vô số nghiệm vì hai đường thẳng biểu diễn các tập nghiệm của hai phương trình trong hệ là trùng nhau.
b) ⇔
⇔
Ta có a = a' = , b = b' = -
nên hai đường thẳng trùng nhau.
Vậy hệ phương trình có vô số nghiệm.
Ta có:
2/(-1) ≠ 1/1 (-2 ≠ 1)
⇒ Hệ phương trình đã cho có nghiệm duy nhất
a)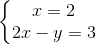
⇔ 
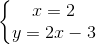
Hệ có nghiệm duy nhất vì một đồ thị là đường thẳng x = 2 song song với trục tung, còn một đồ thị là đường thẳng y = 2x - 3 cắt hai trục tọa độ.
Vẽ (d1): x = 2
Vẽ (d2 ): 2x - y = 3
- Cho x = 0 => y = -3 được A(0; -3).
- Cho y = 0 => x =
được B(
; 0).
Ta thấy hai đường thẳng cắt nhau tại N(2; 1).
Thay x = 2, y = 1 vào phương trình 2x - y - 3 ta được 2 . 2 - 1 = 3 (thỏa mãn).
Vậy hệ phương trình có nghiệm (2; 1).
b)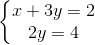
⇔ 
⇔ 
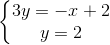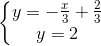
Hệ có nghiệm duy nhất vì một đồ thị là đường thẳng y =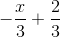
cắt hai trục tọa độ, còn một đồ thị là đường thẳng y = 2 song song vơi trục hoành.
Vẽ (d1): x + 3y = 2
- Cho x = 0 => y =
được A(0; 
).
- Cho y = 0 => x = 2 được B(2; 0).
Vẽ (d2): y = 2
Ta thấy hai đường thẳng cắt nhau tại M(-4; 2).
Thay x = -4, y = 2 vào phương trình x + 3y = 2 ta được -4 + 3 . 2 = 2 (thỏa mãn).
Vậy hệ phương trình có nghiệm (-4; 2).