Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

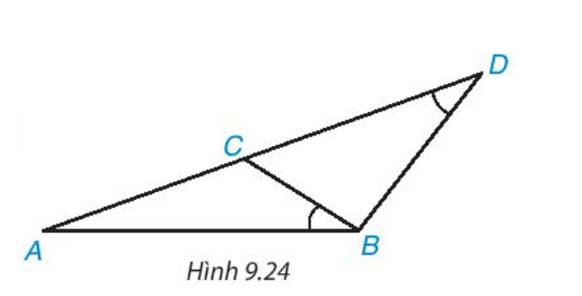
Xét tam giác ABC và tam giác ADB có
\(\widehat {ABC} = \widehat {A{\rm{D}}B}\) và \(\widehat A\) chung
=> ΔABC ∽ ΔADB (g.g)
=> \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\)
=> \(A{B^2} = A{\rm{D}}.AC\)

- Xét tam giác ABD và tam giác ACE có \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\), góc A chung
=> ΔABD ∽ ΔACE (g.g)
- Vì ΔABD ∽ ΔACE
=> \(\widehat {A{\rm{D}}B} = \widehat {A{\rm{E}}C}\)
=> \(\widehat {C{\rm{D}}O} = \widehat {BEO}\) (1)
- Có \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\)
Mà \(\widehat {AB{\rm{D}}} + \widehat {EBO} = {180^o}\)
\(\widehat {AC{\rm{E}}} + \widehat {DCO} = {180^o}\)
=> \(\widehat {EBO} = \widehat {DCO}\) (2)
Từ (1) và (2) => ΔBOE ∽ ΔCOD (g.g)

B K E C H A D M
a)DC//BE (cùng vuông góc với AC);DB//CE (cùng vuông góc với AB) => là hình bình hành
b) hình bình hình thì 2 đường chéo giao nhau tại trung điểm mỗi đường hay DE cắt BC tại M và M là trung điểm DE
Để DE đi qua A tức là D;E;A thằng hàng
mà AE là một đường cao hay AE vuông góc BC nên D;E;A thẳng hàng tức là DE vuông góc với BC
hình bình hành có 2 đường chéo vuông góc là hình thoi
c) tứ giác ABDC có góc DBA +góc DCA =180 nên góc BAC+ góc BDC=180
Mượn hình của bạn Manh nhé!
a) Ta có: DB // CK ( \(\perp\)AB)
=> DB // CE (1)
BH // DC ( \(\perp\) AC )
=> DC // BE (2)
Từ (1) ; (2) => DBEC là hình bình hành.
b) +) Theo câu a) DBEC là hình bình hành
=> Hai đường chéo BC và DE cắt nhau tại trung điểm của mỗi đường.
Mà M là trung điểm BC => M là trung điểm DE.
+) CK; BH là hai đường cao của \(\Delta ABC\) và CK ; BH cắt nhau tại E.
=> E là trực tâm của \(\Delta ABC\)
=> AE là đường cao hạ từ A. (3)
Theo giả thiết DE qua A mà DE cắt BC tại M là trung điểm cạnh BC
=> AE qua trung điểm của cạnh BC
=> AE là đường trung tuyến của \(\Delta ABC\) (4)
Từ (3); (4) => \(\Delta ABC\) cân tại A
c) Em tham khảo bài làm bạn Manh.

Xét \(\Delta ABD\)có: \(\widehat {BAD} + \widehat {ABD} + \widehat {BDA} = {180^0}\)
Xét \(\Delta BCD\)có: \(\widehat {BCD} + \widehat {BDC} + \widehat {DBC} = {180^0}\)
\(\begin{array}{l} \Rightarrow \widehat {BAD} + \widehat {ABD} + \widehat {BDA} = \widehat {BCD} + \widehat {BDC} + \widehat {DBC}\\ \Rightarrow \widehat {DAB} = \widehat {DBC}(do\,\widehat {BAD} = \widehat {BCD};\widehat {ABD} = \widehat {BDC})\end{array}\)
Xét \(\Delta ABD\) và \(\Delta CDB\) có:
\(\begin{array}{l}\left. \begin{array}{l}\widehat {ABD} = \widehat {CDB}\\BDchung\\\widehat {DBA} = \widehat {DBC}\end{array} \right\} \Rightarrow \Delta ABD = \Delta CDB(g.c.g)\\ \Rightarrow AB = DC\\AD = CB\end{array}\)
Suy ra tứ giác ABCD là hình bình hành vì có cặp cạnh đối bằng nhau

a, Tứ giác ABCD có:
\(\widehat {ABC} + \widehat {BCD} + \widehat {CDA} + \widehat {DAB} = {360^0}\)
\(\widehat {ABC} + \widehat {DAB} + \widehat {ABC} + \widehat {DAB} = {360^0}\)(do \(\widehat {DAB} = \widehat {BCD};\widehat {ABC} = \widehat {CDA}\))
\(\begin{array}{l}2\widehat {ABC} + 2\widehat {DAB} = {360^0}\\\widehat {ABC} + \widehat {DAB} = \dfrac{{{{360}^0}}}{2} = {180^0}\end{array}\)
b, Ta có: \(\widehat {xAD} + \widehat {DAB} = {180^0}\)(do tia Ax là tia đối của tia AB)
Nên
\(\begin{array}{l}\widehat {xAD} + \widehat {DAB} = \widehat {ABC} + \widehat {DAB}\\ \Rightarrow \widehat {xAD} = \widehat {ABC}\end{array}\)
Suy ra AD//BC (hai góc đồng vị bằng nhau)
c, Vì AD//BC \( \Rightarrow \widehat {ADB} = \widehat {DBC}\) (2 góc so le trong)
Xét \(\Delta A{\rm{D}}B\) có \(\widehat {ABD} = {180^0} - \widehat {ADB} - \widehat {DAB} = {180^0} - \widehat {DBC} - \widehat {BCD}\left( 1 \right)\)
( vì \(\widehat {ADB} = \widehat {DBC};\widehat {DAB} = \widehat {BCD})\)
Xét \(\Delta CDB\) có: \(\widehat {BDC} = {180^0} - \widehat {DBC} - \widehat {BCD}\left( 2 \right)\)
Từ (1), (2) suy ra \(\widehat {ABD} =\widehat {BDC}\)
Xét \(\Delta ADB\) và \(\Delta BCD\)có:
\(\left. \begin{array}{l}DBchung\\\widehat {ABD} = \widehat {BDC}\\\widehat {ABD} = \widehat {DBC}\end{array} \right\} \Rightarrow \Delta A{\rm{D}}B = \Delta C{\rm{D}}B \Rightarrow A{\rm{D}} = BC,AB = CB\)
Suy ra tứ giác ABCD có cặp cạnh đối bằng nhau nên ABCD là hình bình hành.

a) Xét tam giác \(MNP\) tam giác \(DEF\) ta có:
\(\widehat M = \widehat D\) (giả thuyết)
\(\widehat N = \widehat E\) (giả thuyết)
Do đó, \(\Delta MNP\backsim\Delta DEF\) (g.g)
Suy ra, \(\frac{{MP}}{{DF}} = \frac{{NP}}{{EF}} \Rightarrow \frac{{18}}{{24}} = \frac{{a + 2}}{{32}} \Rightarrow a + 2 = \frac{{18.32}}{{24}} = 24 \Leftrightarrow a = 24 - 2 = 22\).
Vậy \(a = 22m\).
b) Vì \(ABCD\) là hình thang nên \(AB//CD\).
Vì \(AB//CD \Rightarrow \widehat {ABM} = \widehat {MDC}\) (hai góc so le trong) và \(AB//CD \Rightarrow \widehat {BAM} = \widehat {MCD}\) (hai góc so le trong)
Xét tam giác \(AMB\) và tam giác \(CMD\) có:
\(\widehat {ABM} = \widehat {MDC}\) (chứng minh trên)
\(\widehat {BAM} = \widehat {MCD}\) (chứng minh trên)
Do đó, \(\Delta AMB\backsim\Delta CMD\) (g.g).
Ta có:
\(\frac{{AM}}{{CM}} = \frac{{BM}}{{DM}} = \frac{{AB}}{{CD}} \Leftrightarrow \frac{6}{{15}} = \frac{y}{{10}} = \frac{8}{x}\).
Ta có: \(\frac{6}{{15}} = \frac{y}{{10}} \Rightarrow y = \frac{{10.6}}{{15}} = 4\)
\(\frac{6}{{15}} = \frac{8}{x} \Rightarrow x = \frac{{8.15}}{6} = 20\).
Vậy \(x = 20;y = 4\).

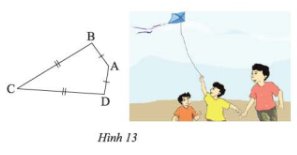
a) Ta có:
\(AB = AD\) (gt) nên \(A\) thuộc đường trung trực của \(BD\)
\(CB = CD\) (gt) nên \(C\) thuộc đường trung trực của \(BD\)
Vậy \(AC\) là đường trung trực của \(BD\)
b) Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = CD\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta ADC\) (c-g-c)
Suy ra: \(\widehat {ABC} = \widehat {ADC} = 95^\circ \) (hai góc tương ứng)
Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên:
\(\widehat A = 360^\circ - \left( {95^\circ + 35^\circ + 95^\circ } \right) = 135^\circ \)

A B C D
a)
Ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Leftrightarrow\frac{C+D}{2}+C+D=360^o\)
\(\Leftrightarrow\frac{3\left(C+D\right)}{2}=360^o\)
\(\Leftrightarrow3\left(C+D\right)=720^o\)
\(\Leftrightarrow C+D=240^o\)
\(\Leftrightarrow A+B=120\)

Xét hai tam giác AEB và DEC có:
\(\widehat {BAC} = \widehat {C{\rm{D}}B}\)(giả thiết)
\(\widehat {AEB} = \widehat {DEC}\) (đối đỉnh)
Suy ra \(\Delta A{\rm{E}}B \backsim \Delta DEC\) suy ra: \(\frac{{A{\rm{E}}}}{{DE}} = \frac{{BE}}{{CE}} \Rightarrow \frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\)
Xét hai tam giác AED và BEC có:
\(\widehat {A{\rm{ED}}} = \widehat {BEC}\) (đối đỉnh)
\(\frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\)
Suy ra ΔAED ∽ ΔBEC (g – c – g)