K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
1
16 tháng 8 2017
Với x/3= y/5 => 5x=3y => x=3y /5
=>x2 = 9y2 /25 . Thay vào A ta được:
A= (5. 9y2 /25 + 3y2) / (10. 9y2 /5 -3y2)
= (9y2 /5 +3y2) / (18y2 /5 -3y2)
= (24/5y2) / (3/5y2) => 24/5 : 3/5 = 8
Vậy A=8
TU
2
12 tháng 3 2017
Đặt \(\frac{x}{3}=\frac{y}{5}=k\Rightarrow x=3k;y=5k\) Thay vào P ta được :
\(P=\frac{5.\left(3k\right)^2+3.\left(5k\right)^2}{10.\left(3k\right)^2-3\left(5k\right)^2}=\frac{45k^2+75k^2}{90k^2-75k^2}=\frac{15k^2\left(3+5\right)}{15k^2\left(6-5\right)}=\frac{3+5}{6-5}=\frac{8}{1}=8\)
Vậy \(P=8\)
17 tháng 8 2017
ta có: x/3=y/5 suy ra x^2 /9=y^2/25
A[s dụng tính chất dãy tỉ số bằng nhau ta có:
x^2/9=y^2/25=(5 x^2 + 3 y^2)/(45+75)=(10 x^2 -3 y^2)/(90-75) do đó (5 x^2 + 3y^2)/(10 x^2 - 3 y^2)=(45+75)/(90-75)=8
XO
1 tháng 8 2020
a) (-xy)10 : (-xy)5 = (-xy)2
b) (5x2y4) : 10x2y = y3/2
c) (15x4y3z2) : (5x2y2z2) = 3x2y
d) \(\frac{3}{4}x^3y^3:\left(-\frac{1}{2}x^2y^2\right)=\frac{\frac{3}{4}x^3y^2}{-\frac{1}{2}x^2y^2}=-\frac{3}{2}x\)
e) 6x3y5 : 12x3y2 = y3/2
f) (25x5 - 5x4 + 10x2) : (5x2)
= 5x3 - x2 + 2
g) \(\frac{2}{3}xy\cdot\left(2x^2y-3xy+y^2\right)=\frac{4}{3}x^3y^2-2x^2y^2+\frac{2}{3}xy^3\)
h) \(\frac{3}{4}x^3y^5z:\left(5x^2y^2z\right)=\frac{\frac{3}{4}x^3y^5z}{5x^2y^2z}=\frac{3}{20}xy^3\)
TT
1
22 tháng 5 2016
a) A+B
A+B=\(\left(x^2-2x-y^2+3y-1\right)\)+\(\left(-2x^2+3y^2-5x+y+3\right)\)
=\(x^2-2x-y^2+3y-1+\left(-2x^2\right)+3y^2-5x+y+3\)
=\(\left(x^2-2x^2\right)+\left(-2x-5x\right)+\left(y^2+3y^2\right)+\left(3y+y\right)+\left(-1+3\right)\)
=\(-x^2-7x+4y^2+4y+2\)
=\(x^2+4y^2-7x+4y+2\)
b) A-B
A-B=\(\left(x^2-2x-y^2+3y-1\right)-\left(-2x^2+3y^2-5x+y+3\right)\)
=\(x^2-2x-y^2+3y-1+2x^2-3y^2+5x-y-3\)
=\(\left(x^2+2x^2\right)+\left(-2x+5x\right)+\left(-y^2-3y^2\right)+\left(3y-y\right)+\left(1-3\right)\)
=\(3x^2+3x-4y^2+2y-2\)
=\(3x^2-4y^2+3x+2y-2\)
mk nha Tân Thái Công Chúa
TQ
3
6 tháng 1 2019
a)\(A=x^3+x^2y-xy-y^2+3y+x-1\)
Ta có:\(x+y-2=0\Rightarrow x+y=2\)
\(A=x^2\left(x+y\right)-y\left(x+y\right)+3y+x-1\)
\(=2x^2-2y+3y+x-1\)
\(=2x^2+y+x-1\)
\(=2x^2+2-1\)
\(=2x^2+1\)
8 tháng 1 2019
b) x - y = 0 => x = y
B = x( x^2 + y^2 ) - y ( x^2 + y^2 ) + 3
= x(x^2 + x^2 ) - x (x^2 + x^2 ) + 3
= 3
10 tháng 8 2019
A = 5x(x - y) - y(5x - y)
A = 5x2 - 5xy - 5xy + y2
A = 5x2 - 10xy + y2 (1)
Thay x = -1; y = 3 vào (1), ta có:
5.(-1)2 - 10.(-1).3 + 32 = 44
B = 4y(x2 - 3xy + 3y2) - 2xy(2x - 6y - 3)
B = 4x2y - 12x2 + 12y3 - 4x2y + 12xy2 + 6xy
B = 12y3 + 6xy (1)
Thay x = 5; y = -1 vào (1), ta có:
12.(-1)3 + 6.5.(-1) = -42
C = 5x2(x - y2) + 3x(xy2 - y) - 5x3
C = 5x3 - 5x2y2 + 3x2y2 - 3xy - 5x3
C = -2x2y2 - 3xy (1)
Thay x = -2; y = -5 vào (1), ta có:
-2.(-2)2.(-5)2 - 3.(-2).(-5) = -230
D = 6x2(y2 - xy + 2x2y) - 3xy(2xy - x2 + 4x3)
D = 6x2y2 - 6x3y + 12x4y - 6x2y2 + 3x3y - 12x4y
D = -3x3y (1)
Thay x = 11; y = -1 vào (1), ta có:
-3.113.(-1) = 3993
3 tháng 10 2016
bn dào khánh linh có vẻ jioi, mk làm 1 câu rùi bn lam tip, nếu k lam dc nt cho mk
a) x/6 = y/10
bn bình phuong tlt trên va nhân 2 ty số đầu mhe:
x/6 = x2/36 = 2x2/72
y/10 = y2/100
đến đây thì dễ rùi, nếu hiu dc thi cám ơn mk đi vi mk dăt tay bn
cung nhau di tren con dg tuoi sang
D
2 tháng 10 2016
a)10x=6y=>\(5x=3y\Rightarrow\frac{x}{3}=\frac{y}{5}=\frac{2x^2-y^2}{18-25}=\frac{-28}{-7}=4\)
b) \(\frac{x^3}{8}=\frac{x}{2}\)
\(\frac{y^3}{64}=\frac{y}{4}\)
\(\frac{z^3}{216}=\frac{z}{6}\)
=>........ áp dụng t.chất dãy tỉ số = nhau
c)
\(\frac{2x+1}{5}=\frac{3y-2}{7}=\frac{2x+3y-1}{6x}=\frac{2x+1+3y-2}{5+7}=\frac{2x+3y-1}{12}\)
=>\(\frac{2x+3y-1}{6x}=\frac{2x+3y-1}{12}\)
=>6x=12( cùng tử)
=>x=2
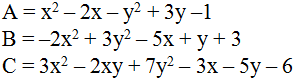
Đặt \(\frac{x}{3}=\frac{y}{5}=k\)
\(\Rightarrow x=3k;y=5k\)
Ta có:
\(B=\frac{5\cdot\left(3k\right)^2+3\left(5k\right)^2}{10\left(3k\right)^2-3\left(5k\right)^2}=\frac{45k^2+75k^2}{90k^2-75k^2}=\frac{120k^2}{15k^2}=8\)
Vậy B=8