Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

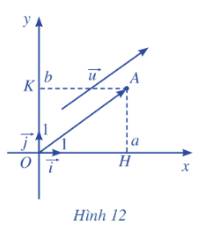
a) Do \(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) nên tọa độ vecto \(\overrightarrow {OA} = \left( {a;b} \right)\). Vậy tọa độ điểm A là: \(A\left( {a;b} \right)\)
b) TỌa độ điểm H là \(H\left( {a;0} \right)\) nên \(\overrightarrow {OH} = \left( {a;0} \right)\). Do đó, \(\overrightarrow {OH} = a\overrightarrow i \)
c) TỌa độ điểm K là \(K\left( {0;b} \right)\) nên \(\overrightarrow {OK} = \left( {0;b} \right)\). Do đó, \(\overrightarrow {OK} = b\overrightarrow j \)
d) Ta có: \({\rm{ }}\overrightarrow u = \overrightarrow {OA} {\rm{ }} = \overrightarrow {OH} + \overrightarrow {OK} = a\overrightarrow i + b\overrightarrow j \) (đpcm)

a) Ta có: \(\overrightarrow u = (2; - 3)\)
\( \Rightarrow \overrightarrow u = 2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j \)
Tương tự ta có: \(\overrightarrow v = (4;1),\;\overrightarrow a = (8; - 12)\)
\( \Rightarrow \overrightarrow v = 4.\;\overrightarrow i + 1.\;\overrightarrow j ;\;\;\overrightarrow a = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \)
b) Ta có: \(\left\{ \begin{array}{l}\overrightarrow u = 2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j \\\overrightarrow v = 4.\;\overrightarrow i + 1.\;\overrightarrow j \end{array} \right.\)(theo câu a)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = \left( {2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j } \right) + \left( {4.\;\overrightarrow i + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u = 4\left( {2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j } \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = \left( {2.\;\overrightarrow i + 4.\;\overrightarrow i } \right) + \left( {\left( { - 3} \right).\;\overrightarrow j + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u = 4.2.\;\overrightarrow i + 4.\left( { - 3} \right).\;\overrightarrow j \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = 6.\;\overrightarrow i + \left( { - 2} \right).\;\overrightarrow j \\4.\;\overrightarrow u = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\end{array}\)
c) Vì \(\left\{ \begin{array}{l}4.\;\overrightarrow u = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \\\overrightarrow a = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\) nên ta suy ra \(4.\;\overrightarrow u = \overrightarrow a \)

a) \(\overrightarrow{a}=2\overrightarrow{u}+3\overrightarrow{v}=2\left(3;-4\right)+3\left(2;5\right)=\left(6;-8\right)+\left(6;15\right)\)\(=\left(12;7\right)\).
b) \(\overrightarrow{b}=\overrightarrow{u}-\overrightarrow{v}=\left(3;-4\right)-\left(2;5\right)=\left(1;-9\right)\).
c) Hai véc tơ \(\overrightarrow{c}=\left(m;10\right)\) và \(\overrightarrow{v}\) cùng phương khi và chỉ khi:
\(\dfrac{m}{2}=\dfrac{10}{5}=2\Rightarrow m=4\).

a) Tọa độ của vectơ \(\overrightarrow u + \overrightarrow v + \overrightarrow w \) là: \(\overrightarrow u + \overrightarrow v + \overrightarrow w = \left( { - 2 + 0 + \left( { - 2} \right);0 + 6 + 3} \right) = \left( { - 4;9} \right)\)
b) Ta có: \(\overrightarrow w + \overrightarrow u = \overrightarrow v \Leftrightarrow \overrightarrow w = \overrightarrow v - \overrightarrow u \) nên \(\overrightarrow w = \left( {0 - \sqrt 3 ; - \sqrt 7 - 0} \right) = \left( { - \sqrt 3 ; - \sqrt 7 } \right)\)

a) \(\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}-4\overrightarrow{c}=3\left(2;1\right)+2\left(3;-4\right)-4\left(-7;2\right)\)
\(=\left(6;3\right)+\left(6;-8\right)-\left(-28;8\right)\)
\(=\left(6+6+28;3-8-8\right)=\left(40;-13\right)\).
b) \(\overrightarrow{x}+\overrightarrow{a}=\overrightarrow{b}-\overrightarrow{c}\Leftrightarrow\overrightarrow{x}=\overrightarrow{b}-\overrightarrow{c}-\overrightarrow{a}\)
\(\Leftrightarrow\overrightarrow{x}=\left(3;-4\right)-\left(-7;2\right)-\left(2;1\right)\)
\(\Leftrightarrow\overrightarrow{x}=\left(3+7-2;-4-2-1\right)\)
\(\Leftrightarrow\overrightarrow{x}=\left(8;-7\right)\).
c) Có \(\overrightarrow{c}\left(-7;2\right)=k\overrightarrow{a}+h\overrightarrow{b}=k\left(2;1\right)+h\left(3;-4\right)\)
\(=\left(2k+3h;k-4h\right)\).
Từ đó suy ra: \(\left\{{}\begin{matrix}2k+3h=-7\\k-4h=2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}k=-2\\h=-1\end{matrix}\right.\).

a) Tọa độ vectơ \(\overrightarrow u = \left( {2.\left( { - 1} \right) + 3 - 3.2;2.2 + 1 - 3.\left( { - 3} \right)} \right) = \left( { - 5;14} \right)\)
b) Do \(\overrightarrow x + 2\overrightarrow b = \overrightarrow a + \overrightarrow c \Leftrightarrow \overrightarrow x = \overrightarrow a + \overrightarrow c - 2\overrightarrow b = \left( { - 1 + 2 - 2.3;2 + \left( { - 3} \right) - 2.1} \right) = \left( { - 5; - 3} \right)\)
Vậy \(\overrightarrow x = \left( { - 5; - 3} \right)\)

A. Ta có: \(\overrightarrow u .\overrightarrow v = 2.4 + 3.6 = 26 \ne 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \) không vuông góc với nhau.
B. Ta có: \(\overrightarrow a .\overrightarrow b = 1.( - 1) + ( - 1).1 = - 2 \ne 0\) nên \(\overrightarrow a \) và \(\overrightarrow b \) không vuông góc với nhau.
C. Ta có: \(\overrightarrow z .\overrightarrow t = a.( - b) + b.a = 0\) nên \(\overrightarrow z \) và \(\overrightarrow t \) vuông góc với nhau.
Chọn đáp án C
D. Ta có: \(\overrightarrow n .\overrightarrow k = 1.2 + 1.0 = 2 \ne 0\) nên \(\overrightarrow n \) và \(\overrightarrow k \) không vuông góc với nhau.

a) Tọa độ của vectơ \(\overrightarrow a \) là \(\left( {2;7} \right)\)
b) Tọa độ của vectơ \(\overrightarrow b \) là \(\left( { - 1;3} \right)\)
c) Tọa độ của vectơ \(\overrightarrow c \) là \(\left( {4;0} \right)\)
d) Tọa độ của vectơ \(\overrightarrow d \) là \(\left( {0; - 9} \right)\)
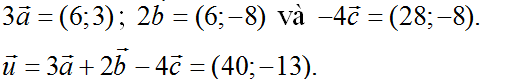
Tham khảo:
a) Trên mặt phẳng tọa độ, lấy các điểm A, B, C sao cho \(\overrightarrow {OA} = \overrightarrow a ;\;\overrightarrow {OB} = \overrightarrow b ;\;\overrightarrow {OC} = \overrightarrow u \)
Trên hệ trục Oxy với các vectơ đơn vị \(\overrightarrow i = \overrightarrow a ,\;\overrightarrow j = \overrightarrow b \), lấy M, N là hình chiếu của C trên Ox, Oy.
Gọi tọa độ của \(\overrightarrow u \)là \(\left( {x;y} \right)\). Đặt \(\alpha = \left( {\overrightarrow u ,\overrightarrow a } \right)\).
+) Nếu \({0^o} < \alpha < {90^o}\): \(x = OM = \;|\overrightarrow u |.\cos \alpha = \;|\overrightarrow u |.\cos \alpha .\;|\overrightarrow a |\; = \overrightarrow u \,.\,\overrightarrow a \,;\)
+) Nếu \({90^o} < \alpha < {180^o}\): \(x = - OM = \; - |\overrightarrow u |.\cos ({180^o} - \alpha ) = \;|\overrightarrow u |.\cos \alpha \; = \overrightarrow u \,.\,\overrightarrow a \,;\)
Như vậy ta luôn có: \(x = \overrightarrow u .\overrightarrow a \)
Chứng minh tương tự, ta có: \(y = \overrightarrow u .\overrightarrow b \)
Vậy vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\)
b) Trong hệ trục Oxy với các vectơ vectơ đơn vị \(\overrightarrow i = \overrightarrow a ,\;\overrightarrow j = \overrightarrow b \), vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\)
\(\begin{array}{l} \Rightarrow \overrightarrow u = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow i + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow j \\ \Leftrightarrow \overrightarrow u = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow a + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow b \end{array}\)