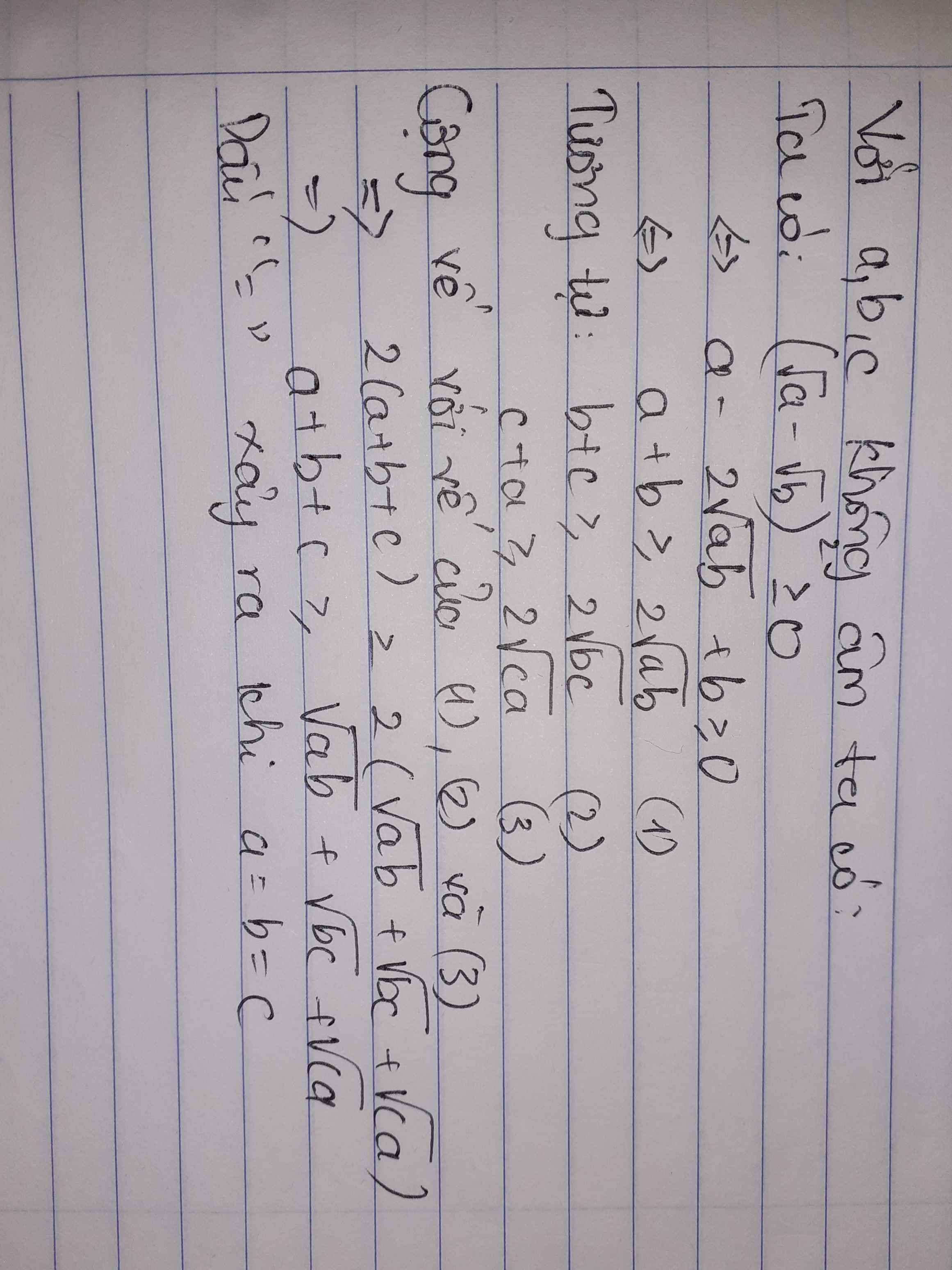Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điều phải chứng minh tương đương với
\(2a+2b+2c-2\sqrt{ab}-2\sqrt{bc}-2\sqrt{ca}\ge0\\ \Leftrightarrow\left(a+b-2\sqrt{ab}\right)+\left(b+c-2\sqrt{bc}\right)+\left(c+a-2\sqrt{ca}\right)\ge0\\ \Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2+\left(\sqrt{b}-\sqrt{c}\right)^2+\left(\sqrt{c}-\sqrt{a}\right)^2\ge0\)
(luôn đúng với mọi a,b,c không âm)
Dấu = xảy ra khi a=b=c >=0

Với mọi số thực x; y; z ta có: \(x^2+y^2+z^2\ge\frac{\left(x+y+z\right)^2}{3}\) ( tự chứng minh xem; có thể áp dụng )
Ta có: \(S^2=\left(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\right)^2\)
\(\le3\left[\left(a+b\right)+\left(b+c\right)+\left(c+a\right)\right]=6\left(a+b+c\right)=6\)
=> \(S\le\sqrt{6}\)
Dấu "=" xảy ra <=> a = b = c =1/3
Vậy max S = \(\sqrt{6}\) tại a = b = c = 1/3.

`A=sqrt{x-2}+sqrt{6-x}(2<=x<=6)`
Áp dụng BĐT `sqrtA+sqrtB>=sqrt{A+B}`
`=>A>=sqrt{x-2+6-x}=2`
Dấu "=" `<=>x=2` hoặc `x=6`
Áp dụng BĐT bunhia
`=>A<=sqrt{2(x-2+6-x)}=2sqrt2`
Dấu "=" `<=>x=4`
`C=sqrt{1+x}+sqrt{8-x}(-1<=x<=8)`
Áp dụng BĐT `sqrtA+sqrtB>=sqrt{A+B}`
`=>A>=sqrt{1+x+8-x}=3`
Dấu "=" `<=>x=-1` hoặc `x=8`
Áp dụng BĐT bunhia
`=>A<=sqrt{2(1+x+8-x)}=3sqrt2`
Dấu "=" `<=>x=7/2`
`D=2sqrt{x+5}+sqrt{1-2x}(-5<=x<=1/2)`
`=sqrt{4x+20}+sqrt{1-2x}`
Áp dụng BĐT `sqrtA+sqrtB>=sqrt{A+B}`
`=>D>=sqrt{4x+20+1-2x}=sqrt{2x+21}`
Mà `x>=-5`
`=>D>=sqrt{-10+21}=sqrt{11}`
Dấu "=" `<=>x=-5`

Lời giải:
Lần sau bạn chú ý gõ đề bài bằng công thức toán!!!
Áp dụng BĐT Cauchy-Schwarz:
\(P=\frac{a}{\sqrt{1-a}}+\frac{b}{\sqrt{1-b}}+\frac{c}{\sqrt{1-c}}=\frac{a}{\sqrt{a+b+c-a}}+\frac{b}{\sqrt{a+b+c-b}}+\frac{c}{\sqrt{a+b+c-c}}\)
\(=\frac{a}{\sqrt{b+c}}+\frac{b}{\sqrt{a+c}}+\frac{c}{\sqrt{a+b}}=\frac{a^2}{a\sqrt{b+c}}+\frac{b^2}{b\sqrt{c+a}}+\frac{c^2}{c\sqrt{a+b}}\)
\(\geq \frac{(a+b+c)^2}{a\sqrt{b+c}+b\sqrt{c+a}+c\sqrt{a+b}}(*)\)
Và:
\((a\sqrt{b+c}+b\sqrt{c+a}+c\sqrt{a+b})^2\leq (a+b+c)(ab+ac+bc+ba+ca+cb)=2(a+b+c)(ab+bc+ac)\)
Áp dụng BĐT AM-GM : \(ab+bc+ac\leq \frac{(a+b+c)^2}{3}\) (quen thuộc)
Do đó:\((a\sqrt{b+c}+b\sqrt{c+a}+c\sqrt{a+b})^2\leq \frac{2}{3}(a+b+c)^3\)
\(\Rightarrow a\sqrt{b+c}+b\sqrt{c+a}+c\sqrt{a+b}\leq \sqrt{\frac{2}{3}(a+b+c)^3}(**)\)
Từ \((*); (**)\Rightarrow P\geq \frac{(a+b+c)^2}{\sqrt{\frac{2}{3}(a+b+c)^3}}=\sqrt{\frac{3}{2}(a+b+c)}=\sqrt{\frac{3}{2}}\)
Vậy \(P_{\min}=\sqrt{\frac{3}{2}}\Leftrightarrow a=b=c=\frac{1}{3}\)
Mình xl vì điện thoại mình kn bấm công thức đk, cảm ơn bạn đã giải và sửa lại đề bài giúp mình nhé!