Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bđt \(\Leftrightarrow\)\(\left(ab+1\right)\left(bc+1\right)\left(ca+1\right)\ge\left(\frac{10}{3}\right)^3abc\) (*)
đặt \(\left(\sqrt{ab};\sqrt{bc};\sqrt{ca}\right)=\left(x;y;z\right)\)\(\Rightarrow\)\(xyz\le\frac{1}{27}\)
(*) \(\Leftrightarrow\)\(\left(x^2+1\right)\left(y^2+1\right)\left(z^2+1\right)\ge\left(\frac{10}{3}\right)^3xyz\)
\(VT\ge\left(xy+1\right)\left(yz+1\right)\left(zx+1\right)\)
Có \(xy+1\ge10\sqrt[10]{\frac{xy}{9^9}}\)
Tương tự với \(yz+1\)\(;\)\(zx+1\)\(\Rightarrow\)\(VT\ge10^3\sqrt[10]{\frac{\left(xyz\right)^2}{9^{27}}}\)
Ta cần CM \(10^3\sqrt[10]{\frac{\left(xyz\right)^2}{9^{27}}}\ge\frac{10^3}{3^3}xyz\) đúng với \(xyz\le\frac{1}{27}\)
Dấu "=" xảy ra khi \(a=b=c=\frac{1}{3}\)
Đặt \(P=\left(a+\frac{1}{b}\right)\left(b+\frac{1}{c}\right)\left(c+\frac{1}{a}\right)\)
Vì a+b+c=1 nên
\(P=\left(a+\frac{1}{b}\right)\left(b+\frac{1}{c}\right)\left(c+\frac{1}{a}\right)=abc+\frac{1}{abc}+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+1\)
Từ BĐt Cosi cho 3 số dương ta có:
\(\frac{1}{3}=\frac{a+b+c}{3}\ge\sqrt[3]{abc}\Rightarrow abc\le\frac{1}{27}\)
đặt x=abc thì \(0< x\le\frac{1}{27}\)
do đó: \(x+\frac{1}{x}-27-\frac{1}{27}=\frac{\left(27-x\right)\left(1-27x\right)}{27x}\ge0\)
=> \(x+\frac{1}{x}=abc+\frac{1}{abc}\ge27+\frac{1}{27}=\frac{730}{27}\)
Mặt khác: \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\Rightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge9\)
Nên \(P\ge\frac{730}{27}+10=\frac{1000}{27}=\left(\frac{10}{3}\right)^3\)
Dấu "=" xảy ra khi a=b=c\(=\frac{1}{3}\)

(a+b) x 2=88 => a+b=44
(b+c) x 2= 148 => b+c=74
(a+c) x 2=108 => a+c=54
(c+d) x 2=208 => c+d=104
(b+d) x 2=188 => b+d=94
(a+d) x 2=148 => a+d= 74
=> a+b+b+c+a+c+c+d+b+d+a+d = 44+74+54+104+94+74
=> 3 x a + 3 x b + 3 x c + 3 x d = 444
3 x (a+b+c+d) = 444
a+b+c+d = 444 : 3
a+b+c+d = 148

Bài 1 :
\(a)\) Ta có :
\(3x=4y=6z\)
\(\Leftrightarrow\)\(\frac{3x}{12}=\frac{4y}{12}=\frac{6z}{12}\)
\(\Leftrightarrow\)\(\frac{x}{4}=\frac{y}{3}=\frac{z}{2}\)
\(\Leftrightarrow\)\(\frac{2x}{8}=\frac{y}{3}=\frac{5z}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2x}{8}=\frac{y}{3}=\frac{5z}{10}=\frac{2x-5z}{8-10}=\frac{-36}{-2}=18\)
Do đó :
\(\frac{x}{4}=18\)\(\Rightarrow\)\(x=18.4=72\)
\(\frac{y}{3}=18\)\(\Rightarrow\)\(y=18.3=54\)
\(\frac{z}{2}=18\)\(\Rightarrow\)\(z=18.2=36\)
Vậy \(x=72\)\(;\)\(y=54\) và \(z=36\)
Chúc bạn học tốt ~
2) Ta có: \(\frac{a}{b+c}=\frac{b}{c+a}=\frac{c}{a+b}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{b+c}=\frac{b}{c+a}=\frac{c}{a+b}=\frac{a+b+c}{b+c+c+a+a+b}=\frac{a+b+c}{2.\left(a+b+c\right)}=\frac{1}{2}\)
\(\Rightarrow\frac{a}{b+c}=\frac{1}{2}\Rightarrow2a=b+c\)
\(\frac{b}{c+a}=\frac{1}{2}\Rightarrow2b=c+a\)
\(\frac{c}{a+b}=\frac{1}{2}\Rightarrow2c=a+b\)
Ta có: \(\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right)=\frac{b+a}{b}.\frac{c+b}{c}.\frac{a+c}{a}=\frac{2c.2a.2b}{b.c.a}=8\)
Vậy \(\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right)=8\)

\(\left(1+\frac{1}{2}\right)\left(1+\frac{1}{3}\right)\left(1+\frac{1}{4}\right)...\left(1+\frac{1}{99}\right)\)
\(=\frac{3}{2}\times\frac{4}{3}\times...\times\frac{100}{99}\)
\(=\frac{100}{2}=50\)

Ta có:
\(A=\frac{\frac{1}{2001}+\frac{1}{2002}+...+\frac{1}{4000}}{\frac{1}{1.2}+\frac{1}{3.4}+...+\frac{1}{3999.4000}}\)
\(=\frac{\frac{1}{2001}+\frac{1}{2002}+...+\frac{1}{4000}}{\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{3999}-\frac{1}{4000}}\)
\(=\frac{\frac{1}{2001}+\frac{1}{2002}+...+\frac{1}{4000}}{\left(1+\frac{1}{3}+...+\frac{1}{3999}\right)-\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{4000}\right)}\)
\(=\frac{\frac{1}{2001}+\frac{1}{2002}+...+\frac{1}{4000}}{\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{3999}+\frac{1}{4000}\right)-2.\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{4000}\right)}\)
\(=\frac{\frac{1}{2001}+\frac{1}{2002}+...+\frac{1}{4000}}{\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{3999}+\frac{1}{4000}\right)-\left(1+\frac{1}{2}+...+\frac{1}{2000}\right)}\)
\(=\frac{\frac{1}{2001}+\frac{1}{2002}+...+\frac{1}{4000}}{\frac{1}{2001}+\frac{1}{2002}+...+\frac{1}{4000}}=1\)
Ta lại có:
\(B=\frac{\left(17+1\right)\left(\frac{17}{2}+1\right)...\left(\frac{17}{19}+1\right)}{\left(1+\frac{19}{17}\right)\left(1+\frac{19}{16}\right)...\left(1+19\right)}\)
\(=\frac{\frac{18}{1}.\frac{19}{2}.\frac{20}{3}...\frac{36}{19}}{\frac{36}{17}.\frac{35}{16}.\frac{34}{15}...\frac{20}{1}}\)
\(=\frac{1.2.3...36}{1.2.3...36}=1\)
Từ đây ta suy ra được
\(A-B=1-1=0\)

a) \(\dfrac{2}{3}\times\dfrac{4}{5}=\dfrac{4}{5}\times\dfrac{2}{3}\)
b) \(\left(\dfrac{1}{3}\times\dfrac{2}{5}\right)\times\dfrac{3}{4}=\dfrac{1}{3}\times\left(\dfrac{2}{5}\times\dfrac{3}{4}\right)\)
c) \(\left(\dfrac{1}{3}-\dfrac{2}{15}\right)\times\dfrac{3}{4}=\dfrac{1}{3}\times\dfrac{3}{4}+\dfrac{2}{15}\times\dfrac{3}{4}\)

a: Ta có:
\(\left(\dfrac{2}{5}+\dfrac{1}{5}\right)+\dfrac{1}{5}=\dfrac{3}{5}+\dfrac{1}{5}=\dfrac{4}{5}\)
\(\dfrac{2}{5}+\left(\dfrac{1}{5}+\dfrac{1}{5}\right)=\dfrac{2}{5}+\dfrac{2}{5}=\dfrac{4}{5}\)
\(\dfrac{4}{5}=\dfrac{4}{5}\). Vậy \(\left(\dfrac{2}{5}+\dfrac{1}{5}\right)+\dfrac{1}{5}=\dfrac{2}{5}+\left(\dfrac{1}{5}+\dfrac{1}{5}\right)\)
Ta có:
\(\left(\dfrac{2}{9}+\dfrac{5}{9}\right)+\dfrac{1}{9}=\dfrac{7}{9}+\dfrac{1}{9}=\dfrac{8}{9}\)
\(\dfrac{2}{9}+\left(\dfrac{5}{9}+\dfrac{1}{9}\right)=\dfrac{2}{9}+\dfrac{6}{9}=\dfrac{8}{9}\)
\(\dfrac{8}{9}=\dfrac{8}{9}\). Vậy \(\left(\dfrac{2}{9}+\dfrac{5}{9}\right)+\dfrac{1}{9}=\dfrac{2}{9}+\left(\dfrac{5}{9}+\dfrac{1}{9}\right)\)
b: \(\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\dfrac{4}{3}=\dfrac{3}{3}+\dfrac{4}{3}=\dfrac{7}{3}\)
\(\dfrac{1}{3}+\left(\dfrac{2}{3}+\dfrac{4}{3}\right)=\dfrac{1}{3}+\dfrac{6}{3}=\dfrac{7}{3}\)
\(\dfrac{7}{3}=\dfrac{7}{3}\). Vậy \(\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\dfrac{4}{3}=\dfrac{1}{3}+\left(\dfrac{2}{3}+\dfrac{4}{3}\right)\)
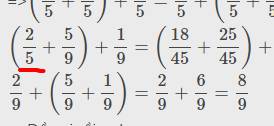
Đề của anh bị sai mới đúng chứ ạ? Anh Đạt ghi là \(\left(\dfrac{2}{9}+\dfrac{5}{9}\right)+\dfrac{1}{9}\) chứ có phải \(\dfrac{2}{5}\) đâu ạ?



Đặt \(a+b-c=x;b+c-a=y;a+c-b=z\)
BĐT <=> \(\left(x+y+z\right)^3xyz\le27.\left(\frac{x+z}{2}\right)^2\left(\frac{y+z}{2}\right)^2\left(\frac{x+y}{2}\right)^2\)
<=> \(64xyz\left(x+y+z\right)^3\le\left[\left(x+y\right)\left(y+z\right)\left(x+z\right)\right]^2\)(1)
Xét \(\left(x+y\right)\left(y+z\right)\left(x+z\right)\ge\frac{8}{9}\left(x+y+z\right)\left(xy+yz+xz\right)\)
<=> \(9\left[xy\left(x+y\right)+yz\left(y+z\right)+xz\left(x+z\right)+2xyz\right]\ge8\left[xy\left(x+y\right)+...+3xyz\right]\)
<=> \(xy\left(x+y\right)+xz\left(x+z\right)+yz\left(y+z\right)\ge6xyz\)(luôn đúng )
vì \(VT\ge3\sqrt[3]{x^2y^2z^2.\left(x+y\right)\left(y+z\right)\left(x+z\right)}\ge6xyz\)
Khi đó BĐT (1)
<=> \(64.xyz\left(x+y+z\right)^3\le27\left[\frac{8}{9}\left(x+y+z\right)\left(xy+yz+xz\right)\right]^2\)
<=> \(3xyz\left(x+y+z\right)\le\left(xy+yz+xz\right)^2\)
<=> \(x^2y^2+y^2z^2+x^2z^2\ge xyz\left(x+y+z\right)\)(BĐT Cosi)
=> BĐT được Cm
Dấu bằng xảy ra khi a=b=c
Mình có cách khác
bđt đồng bật nên t chuẩn hóa \(a+b+c=1\)
Ta biến doi vế trái về: \(\left[\left(a+b\right)^2-c^2\right]\left[\left(b+c\right)^2-a^2\right]\left[\left(c+a\right)^2-b^2\right]\)
\(=\left[\left(1-c\right)^2-c^2\right]\left[\left(1-a\right)^2-a^2\right]\left[\left(1-b\right)^2-b^2\right]\)
Giờ ta cần chứng minh:\(\left[\left(1-c\right)^2-c^2\right]\left[\left(1-a\right)^2-a^2\right]\left[\left(1-b^2\right)-b^2\right]\le27a^2b^2c^2\)
Ta xét :\(0< a,b,c< \frac{1}{3}\)(*)
\(\Rightarrow a+b+c< 1\)
vì \(a+b+c=1\)nên (*) vô lý
Ta xét:\(\frac{1}{3}\le a,b,c< 1\)
Đến đây ta thấy giữa các biến có sự riêng biệt nên ta xét:
\(3a^2-\left[\left(1-a\right)^2-a^2\right]=\left(3a-1\right)\left(a+1\right)\ge0\)
\(\Rightarrow3a^2\ge\left(1-a\right)^2-a^2\)
Tương tự:\(3b^2\ge\left(1-b\right)^2-b^2\)
\(3c^2\ge\left(1-c\right)^2-c^2\)
nhan các vế bđt lại với nhau ta có điều phải chứng minh
Đến đây ta có thể suy ra điều phải chứng minh
vài lời nhắn:
Mình không chắt về cách xét của mình nữa