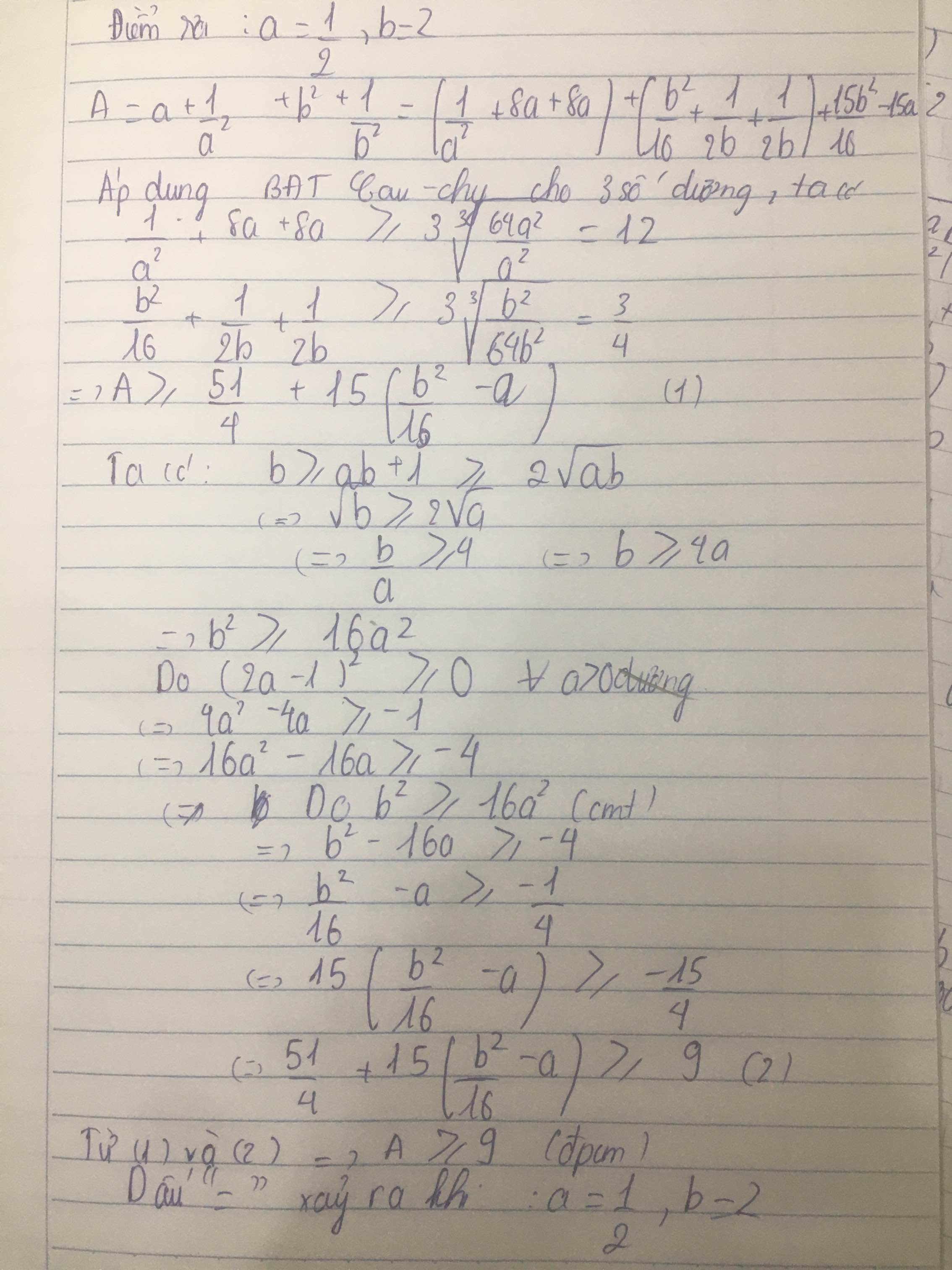P
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
P
0
PN
28 tháng 7 2016
Keke
\(\frac{1}{a}+\frac{2}{b}+\frac{3}{c}\ge\frac{3}{a+b}+\frac{18}{3b+4c}+\frac{9}{c+6a}\) \(\left(i\right)\)
Đặt \(x=\frac{1}{a};\) \(y=\frac{2}{b};\) và \(z=\frac{3}{c}\) \(\Rightarrow\) \(\hept{\begin{cases}a=\frac{1}{x}\\b=\frac{2}{b}\\c=\frac{3}{z}\end{cases}}\) nên \(x,y,z>0\)
Khi đó, ta có thể biểu diễn lại bđt \(\left(i\right)\) dưới dạng ba biến \(x,y,z\) như sau:
\(x+y+z\ge\frac{3xy}{2x+y}+\frac{3yz}{2y+z}+\frac{3xz}{2z+x}\) \(\left(ii\right)\)
Lúc này, ta cần phải chứng minh bđt \(\left(ii\right)\) luôn đúng với mọi \(x,y,z>0\)
Thật vậy, ta có:
\(2x+y=x+x+y\ge3\sqrt[3]{x^2y}\)
\(\Rightarrow\) \(\frac{3xy}{2x+y}\le\frac{3xy}{3\left(x^2y\right)^{\frac{1}{3}}}=\left(xy^2\right)^{\frac{1}{3}}\le\frac{x+2y}{3}\) \(\left(1\right)\)
Thiết lập các bđt còn lại theo vòng hoán vị \(y\rightarrow z\rightarrow x\) , ta có:
\(\frac{3yz}{2y+z}\le\frac{y+2z}{3}\) \(\left(2\right);\) \(\frac{3xz}{2z+x}\le\frac{z+2x}{3}\) \(\left(3\right)\)
Cộng từng vế ba bđt \(\left(1\right);\) \(\left(2\right);\) và \(\left(3\right)\) ta được:
\(VP\left(ii\right)\le\frac{x+2y+y+2z+z+2x}{3}=\frac{3\left(x+y+z\right)}{3}=x+y+z=VT\left(ii\right)\)
Vậy, bđt \(\left(ii\right)\) được chứng minh.
nên kéo theo bđt \(\left(i\right)\) luôn là bđt đúng với mọi \(a,b,c>0\)
Dấu \("="\) xảy ra \(\Leftrightarrow\) \(x=y=z\) \(\Leftrightarrow\) \(6a=3b=2c\)
23 tháng 2 2019
1)a)Ta có:\(a^3-13a=a^3-a-12a=\left(a-1\right)a\left(a+1\right)-12a\)
Ta có:\(\left(a-1\right)a\left(a+1\right)⋮\)2 và 3;\(12a⋮6\)
Mà (2;3)=1\(\Rightarrow\left(a-1\right)a\left(a+1\right)⋮6\)
\(\Rightarrow\left(a-1\right)a\left(a+1\right)-12a⋮6\left(đpcm\right)\)
b)Hình như đề sai
C6. Cho các số thực dương thoả mãn: ab+1 nhỏ hơn hoặc bằng b Chứng minh rằng : ( a + (1/a^2) ) + ( b^2 + (1/b) ) lớn hơn hoặc bằng 9
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
\(ab+1\le b\Rightarrow a+\dfrac{1}{b}\le1\)
Đặt \(\left(a;\dfrac{1}{b}\right)=\left(x;y\right)\Rightarrow x+y\le1\)
Gọi vế trái của BĐT cần chứng minh là P:
\(P=x+\dfrac{1}{x^2}+y+\dfrac{1}{y^2}=\left(\dfrac{1}{x^2}+8x+8x\right)+\left(\dfrac{1}{y^2}+8y+8y\right)-15\left(x+y\right)\)
\(P\ge3\sqrt[3]{\dfrac{64x^2}{x^2}}+3\sqrt[3]{\dfrac{64y^2}{y^2}}-15.1=9\) (đpcm)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{1}{2};\dfrac{1}{2}\right)\) hay \(\left(a;b\right)=\left(\dfrac{1}{2};2\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1 2021
Đặt vế trái của BĐT là P:
\(P=\sqrt{\left(a+2\right)\left(b+2\right)}+\sqrt{2b.\left(a+1\right)}\)
\(P\le\dfrac{1}{2}\left(a+2+b+2\right)+\dfrac{1}{2}\left(2b+a+1\right)\)
\(P\le\dfrac{1}{2}\left(2a+3b+5\right)=\dfrac{1}{2}.2024=1012\)
Dấu "=" không xảy ra
1 tháng 4 2021
\(\frac{a+3c}{a+b}+\frac{a+3b}{a+c}+\frac{2a}{b+c}\)
\(=\frac{a+c+2c}{a+b}+\frac{a+b+2b}{a+c}+\frac{2a}{b+c}\)
\(=\frac{a+c}{a+b}+\frac{2c}{a+b}+\frac{a+b}{a+c}+\frac{2b}{a+c}+\frac{2a}{b+c}\)
\(=\left(\frac{a+c}{a+b}+\frac{a+b}{a+c}\right)+2\left(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\right)\)
Áp dụng bất đẳng thức AM-GM ta có :
\(\frac{a+c}{a+b}+\frac{a+b}{a+c}\ge2\sqrt{\frac{a+c}{a+b}\cdot\frac{a+b}{a+c}}=2\)
Cần chứng minh \(2\left(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\right)\ge3\)thì bài toán được chứng minh
tức là \(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\ge\frac{3}{2}\)
Tuy nhiên đây là bất đẳng thức Nesbitt quen thuộc nên ta có điều phải chứng minh
Đẳng thức xảy ra <=> a=b=c