Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


tập hợp N là số nguyên (1)
mà A = giá tri nguyên (2)
và x < 30 (3)
từ (1),(2),(3) ta có:
x={0;1;2;3;...;29}

TL :
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt

Cái bài này mình đã từng đăng để hỏi mấy bạn kia.
Nhưng đề câu này thiểu bạn ơi.
Phải có x=a/m ; y=b/m
À thôi, mk viết đầy đủ đề thử nhé !
Giả sử:x=a/m;y=b/m (a,b,m thuộc Z.m > 0) và x < y.
Hãy chứng minh (chứng tỏ) rằng nếu chọn z=a+b/2m thì ta có x < y < z.
Trong sách lớp 7 đề y như z đó !
Mk ghi cách làm luôn nha !
Giả sử x=a/m,y=b/m (a,b,m thuộc Z,m > 0 )
Vì x < y nên ta suy ra a < b.
ta có: x=a/m, y=b/m <=> x=2a/am. y=2b/2m
mà a < b nên a+a < a+b <=> 2a < a+b
Do 2a < a+b thì x < y ( 1 )
Ta lại có: a < b nên a+b < b+b <=> a+b < 2b
Mà a+b < 2b <=> x < z ( 2 )
Từ ( 1 ) và ( 2 ) suy ra x < y < z (ĐPCM)

a. Xét ΔAMB và ΔAMC, ta có:
AM = AC (gt)
BM = CM (gt)
AM cạnh chung
Suy ra: ΔAMB = ΔAMC (c.c.c)
Suy ra: ∠(AMB) = ∠(AMC) (1)
Lại có: ∠(AMB) + ∠(AMC) = 180o (hai góc kề bù) (2)
Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90o
Vậy AM ⊥ BC.
b. Tam giác AMB có ∠(AMB) = 90o
Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:
AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162
= 1156 - 256 = 900
Suy ra: AM = 30 (cm).

\(\frac{2}{4}=\frac{3}{6}=\frac{2+3}{4+6}\)
\(\frac{2}{4}=\frac{3}{6}=\frac{2-3}{4-6}\)
\(\Rightarrow\frac{2+3}{4+6}=\frac{2-3}{4-6}\)

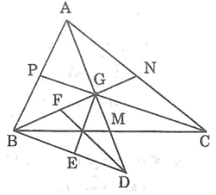
a. Gọi AM, BN, CP lần lượt là các đường trung tuyến của ΔABC. Các đường trung tuyến cắt nhau tại G.
Ta có: AG = GD (gt)
AG = 2GM (tính chất đường trung tuyến)
Suy ra: GD = 2GM
Mà GD = GM + MD ⇒ GM = MD
Xét ΔBMD và ΔCMG, ta có:
BM = CM (gt)
∠(BMD) = ∠(CMG) (đối đỉnh)
MD = GM (chứng minh trên)
Suy ra: ΔBMD = ΔCMG (c.g.c)
⇒ BD = CG (hai cạnh tương ứng)
Mặt khác: CG = 2/3 CP (tính chất đường trung tuyến)
Suy ra: BD = 2/3 CP (1)
Lại có: BG = 2/3 BN (tính chất đường trung tuyến) (2)
Và AG = 2/3 AM (tính chất đường trung tuyến)
Suy ra: GD = 2/3 AM (3)
Từ (1), (2) và (3) suy ra các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.
b. Ta có: GM = MD (chứng minh trên)
Suy ra BM là đường trung tuyến của tam giác BGD.
Suy ra: BM = 1/2 BC (4)
Kẻ đường trung tuyến GE và DF của tam giác BGD, ta có:
FG = 1/2 BG (tính chất đường trung tuyến)
GN = 1/2 GB (tính chất đường trung tuyến)
Suy ra: FG = GN
Xét ΔDFG và ΔANG, ta có:
AG = GD (gt)
∠(DGF) = ∠(AGN) (đối đỉnh)
GF = GN (chứng minh trên)
Suy ra: ΔDFG = ΔANG (c.g.c) ⇒ DF = AN
Mà AN = 1/2 AC (gt)
Suy ra: DF = 1/2 AC (5)
Mặt khác: BD = CG (chứng minh trên)
ED = 1/2 BD (vì E là trung điểm BD)
GP = 1/2 CG (tính chất đường trung tuyến)
Suy ra: ED = GP
Lại có: ΔBMD = ΔCMG (chứng minh trên)
⇒ ∠(BDM) = ∠(CGM) hay ∠(EDG) = ∠(CGM)
(CGM) = (PGA) (đối đỉnh)
Suy ra: ∠(EDG) = ∠(PGA)
AG = GD (gt)
Suy ra: ΔPGA = ΔEDG (c.g.c) ⇒ GE = AP mà AP = 1/2 AB (gt)
Do đó: GE = 1/2 AB(6)
Từ (4), (5) và (6) suy ra các đường trung tuyến của ΔBGD bằng một nửa cạnh của ΔABC.
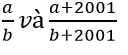

 (a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn 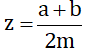 thì ta có x < z < y.
thì ta có x < z < y.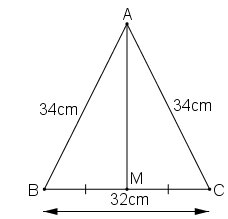
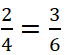
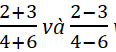 với các tỉ số trong tỉ lệ thức đã cho.
với các tỉ số trong tỉ lệ thức đã cho.