
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

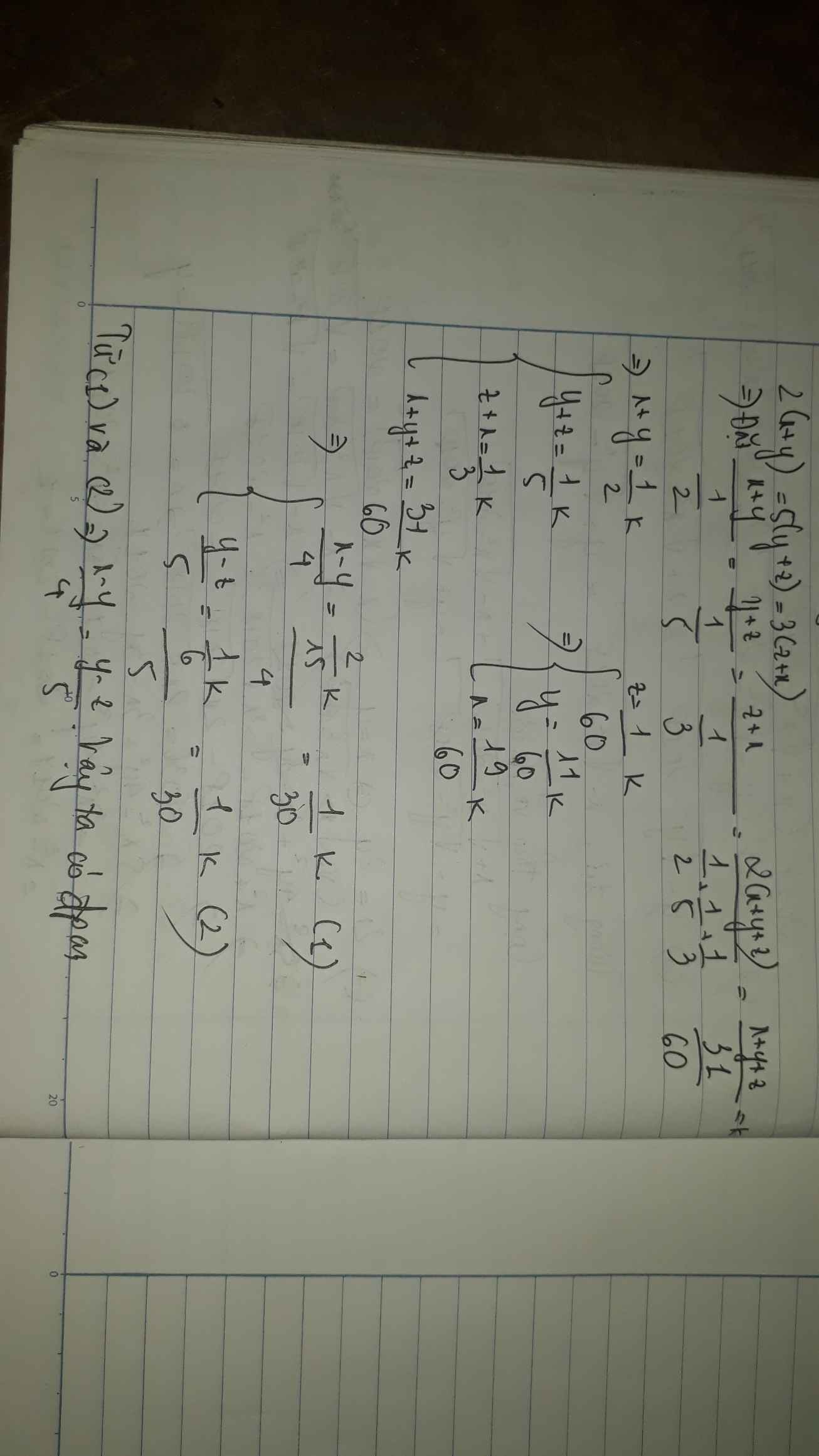

\(\frac{x}{1998}=\frac{y}{1999}=\frac{z}{2000}=t=\frac{x-z}{1998-2000}=\frac{x-y}{1998-1999}=\frac{y-z}{1999-2000}.\)
Hay: \(\frac{x-z}{-2}=\frac{x-y}{-1}=\frac{y-z}{-1}\Rightarrow x-z=2\left(x-y\right)=2\left(y-z\right)\)(1)
a) \(\left(x-z\right)^3=\left(x-z\right)^2\left(x-z\right)=\left(2\left(x-y\right)\right)^2\left(2\left(y-z\right)\right)\)
\(\Leftrightarrow\left(x-z\right)^3=8\left(x-y\right)^2\left(y-z\right)\)ĐPCM a)
b) Từ (1) => x + z = 2y
Để \(2\left(x+y\right)=5\left(y+z\right)=3\left(z+x\right)\Rightarrow\frac{x+y}{\frac{1}{2}}=\frac{y+z}{\frac{1}{5}}=\frac{z+x}{\frac{1}{3}}\)
Từ \(\Rightarrow\frac{x+y}{\frac{1}{2}}=\frac{y+z}{\frac{1}{5}}=\frac{x+y+y+z}{\frac{1}{2}+\frac{1}{5}}=\frac{4y}{\frac{7}{10}}=\frac{2y}{\frac{1}{3}}\)
=>y=0 =>x=0 => z=0 Suy ra hệ thức: x-y/4=y-z/5 luôn đúng. ĐPCM

Ta có \(2\left(x+y\right)=5\left(y+z\right)=3\left(z+x\right)\)
\(\Leftrightarrow\frac{2\left(x+y\right)}{30}=\frac{5\left(y+z\right)}{30}=\frac{3\left(x+z\right)}{30}\)
\(\Rightarrow\frac{x+y}{15}=\frac{y+z}{6}=\frac{z+x}{10}\)
Xét \(\frac{z+x}{10}=\frac{y+z}{6}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{z+x}{10}=\frac{y+z}{6}=\frac{\left(z+x\right)-\left(y+z\right)}{4}=\frac{x-y}{4}\) (1)
Xét \(\frac{x+y}{15}=\frac{z+x}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x+y}{15}=\frac{z+x}{10}=\frac{\left(x+y\right)-\left(z+x\right)}{5}=\frac{y-z}{5}\) (2)
Từ (1) và (2)
\(\Rightarrow\frac{x-y}{4}=\frac{y-z}{5}\)

Từ 2.(x + y)= 5(y + z) = 3(z + x) => \(\frac{2\left(x+y\right)}{30}=\frac{5\left(y+z\right)}{30}=\frac{3\left(z+x\right)}{30}\) => \(\frac{x+y}{15}=\frac{y+z}{6}=\frac{z+x}{10}\)
Áp dụng t/c của dãy tỉ số bằng nhau ta có: \(\frac{x+y}{15}=\frac{y+z}{6}=\frac{z+x}{10}=\frac{\left(x+z\right)-\left(y+z\right)}{10-6}=\frac{\left(x+y\right)-\left(z+x\right)}{15-10}\)
=> \(\frac{x-y}{4}=\frac{y-z}{5}\) => \(\frac{x-y}{y-z}=\frac{4}{5}\)
Vậy...


Ta có: \(2\left(x+y\right)=5\left(y+z\right)=3\left(z+x\right)\)
\(\Rightarrow\frac{2\left(x+y\right)}{30}=\frac{5\left(y+z\right)}{30}=\frac{3\left(z+x\right)}{30}\)
\(\Rightarrow\frac{x+y}{15}=\frac{y+z}{6}=\frac{z+x}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x+y}{15}=\frac{y+z}{6}=\frac{z+x}{10}=\frac{x+y-z-x}{15-10}=\frac{z+x-y-z}{10-6}=\frac{y-z}{5}=\frac{x-y}{4}\left(đpcm\right)\)
Ta có: \(2\left(x+y\right)=5\left(y+z\right)=3\left(x+z\right)\Rightarrow\frac{2\left(x+y\right)}{30}=\frac{5\left(y+z\right)}{30}=\frac{3\left(x+z\right)}{30}\)
\(\Rightarrow\frac{x+y}{15}=\frac{y+z}{6}=\frac{x+z}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{x+y}{15}=\frac{y+z}{6}=\frac{x+z}{10}=\frac{x+z-y-z}{10-6}=\frac{x+y-x-z}{15-10}=\frac{x-y}{4}=\frac{y-z}{5}\left(đpcm\right)\)

2 . ( x + y ) = 5 . ( y + z ) = 3 . ( z + x )
\(\Rightarrow\frac{2.\left(x+y\right)}{30}=\frac{5.\left(y+z\right)}{30}=\frac{3.\left(z+x\right)}{30}\)
\(\Rightarrow\frac{x+y}{15}=\frac{y+z}{6}=\frac{z+x}{10}\)
\(\frac{x+y}{15}=\frac{z+x}{10}=\frac{\left(x+y\right)-\left(z+x\right)}{15-10}=\frac{y-z}{5}\left(1\right)\)
\(\frac{z+x}{10}=\frac{y+z}{6}=\frac{\left(z+x\right)-\left(y+z\right)}{10-6}=\frac{x-y}{4}\left(2\right)\)
Từ ( 1 ) và ( 2 ) \(\Rightarrow\frac{y-z}{5}=\frac{x-y}{4}\)

Vì 5(y+z) = 3(x+z)
Suy ra (x+z) / 5 = (y+z) / 3 = (x+z-y-z) / 5-3 = (x-y) / 2
Suy ra (x+z) / 5 = (x-y) / 2 tương đương (x+z) / 10 = (x-y) / 4 (1)
2(x+y) = 3(x+z)
Suy ra (x+z) / 2 = (x+y) / 3 = (x+z-x-y) / 2-3 = y-z
(x+z) / 2 = y-z
Tương đương (x+z) / 10 = (y-z) / 5 (2)
Từ (1) và (2) suy ra:
Cop mạng ghi nguồn đầy đủ vào nhé!
Ta có: \(2\left(x+y\right)=3\left(z+x\right)\)
\(\Rightarrow\frac{x+y}{3}=\frac{z+x}{2}\)
\(=\frac{x+y-\left(z+x\right)}{3-2}=y-z\)(tính chất dãy tỉ số bằng nhau)
\(\Rightarrow\frac{x+z}{2}=y-z\)
\(\Rightarrow\frac{x+z}{10}=\frac{y-z}{5}\left(1\right)\)
Lại có:\(5\left(y+z\right)=3\left(x+z\right)\)
\(\Rightarrow\frac{y+z}{3}=\frac{x+z}{5}\)
\(=\frac{z+x-\left(y+z\right)}{5-3}=\frac{x-y}{2}\)
\(\Rightarrow\frac{x+z}{5}=\frac{x-y}{2}\)
\(\Rightarrow\frac{x+z}{10}=\frac{x-y}{4}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\frac{x-y}{4}=\frac{y-z}{5}\left(đpcm\right)\)

Câu hỏi của Nguyễn Quang Tùng - Toán lớp 7 - Học toán với OnlineMath

ta có: \(5.\left(y+z\right)=3.\left(z+x\right)\)
\(\Rightarrow\frac{z+x}{5}=\frac{y+z}{3}=\frac{z+x-y-z}{5-3}=\frac{x-y}{2}\)
\(\Rightarrow\frac{z+x}{5}=\frac{x-y}{2}\Rightarrow\frac{1}{2}.\frac{z+x}{5}=\frac{1}{2}.\frac{x-y}{2}=\frac{z+x}{10}=\frac{x-y}{4}\) (1)
ta có: \(2.\left(x+y\right)=3.\left(z+x\right)\)
\(\Rightarrow\frac{x+y}{3}=\frac{z+x}{2}=\frac{x+y-z-x}{3-2}=\frac{y-z}{1}=y-z\)
\(\Rightarrow\frac{z+x}{2}=y-z\Rightarrow\frac{1}{5}.\frac{z+x}{2}=\frac{1}{5}.\left(y-z\right)\Rightarrow\frac{z+x}{10}=\frac{y-z}{5}\)(2)
Từ (1);(2) \(\Rightarrow\frac{x-y}{4}=\frac{y-z}{5}\left(=\frac{z+x}{10}\right)\) ( đ p c m)
Ta có: \(2\left(x+y\right)=5\left(y+z\right)=3\left(z+x\right)\)
\(\Rightarrow\frac{2\left(x+y\right)}{30}=\frac{5\left(y+z\right)}{30}=\frac{3\left(z+x\right)}{30}\)
\(\Rightarrow\frac{x+y}{15}=\frac{y+z}{6}=\frac{z+x}{10}=\frac{x+y-\left(z+x\right)}{15-10}=\frac{z+x-\left(y+z\right)}{10-6}\)
\(\Rightarrow\frac{x-y}{4}=\frac{y-z}{5}\)