Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

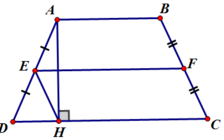
*Có AH ⊥ CD ⇒ ∆ AHD vuông tại H
E là trung điểm của AD ⇒ HE là trung tuyến ứng với cạnh huyền AD
⇒ HE = 1/2 AD (1)
*F là trung điểm của BC ⇒ CF = 1/2 BC (2)
Mà ABCD là hình thang cân ⇒ BC = AD (3)
Từ (1), (2) và (3) ta có: HE = CF (*)
*Mặt khác: EH = ED = 1/2 AD (Chứng minh trên)
⇒ ∆ EHD cân tại E
⇒ ∠ (EHD) = ∠ (EDH)
Mà ∠ (EDH) = ∠ (FCH) (góc đáy hình thang cân)
⇒ ∠ (FCH) = ∠ (EHD) (cùng bằng ∠ (EDH))
⇒EH // FC (2 góc ở vị trí đồng vị bằng nhau) (**)
Từ (*) và (**) ⇒ EFCH là hình bình hành (1 cặp cạnh song song và bằng nhau)

Ta có:
E là trung điểm của AD (gt), F là trung điểm của BC (gt) nên EF là đường trung bình của hình thang ABCD.
\(\Rightarrow\) EF // CD hay EF // CH.
\(\Delta\)AHD vuông tại H có HE là đường trung tuyến thuộc cạnh huyền AD.
Ta có: HE = ED = \(\frac{1}{2}\) AD (tính chất tam giác vuông)
\(\Rightarrow\Delta\) EDH cân tại E \(\Rightarrow\widehat{D}\) = \(\widehat{H}\) 1(tính chất tam giác cân)
\(\widehat{D}\)=\(\widehat{C}\)(vì ABCD là hình thang cân)
\(\Rightarrow\)\(\widehat{H}\)1 = \(\widehat{C}\)\(\Rightarrow\) EH // CF (vì có cặp góc đồng vị bằng nhau)
Vậy tứ giác EFCH là hình bình hành.
#Trang

A B C D P Q E F
a) Có \(DE=\frac{1}{2}DA\), \(BF=\frac{1}{2}BC\).
Tứ giác ABCD là hình bình hành nên DE = BC suy ra DE = BF.
Mà DE // BF.
Vì vậy tứ giác BEDF là hình bình hành.
b) Theo chứng minh câu a tứ giác BEDF là hình bình hành suy ra BE // DF.
Xét tam giác ADQ có E là trung điểm của DA và AB // DQ nên P là trung điểm của AQ.
Vì vậy AP = PQ. (1)
Xét tam giác BCP có F là trung điểm của BC và FD // BE nên Q là trung điểm của của PC.
Vì vậy PQ = QC. (2)
Từ (1) và (2) suy ra: AP = PQ = QC.
c)Do AE // BC nên áp dụng định lý Ta-lét:
\(\frac{AP}{PB}=\frac{EP}{PB}=\frac{1}{2}\).
Suy ra \(EP=\frac{1}{2}PB\).
Mặt khác R là trung điểm của PB nên PR = RB \(=\frac{1}{2}PB\).
Từ đó suy ra \(EP=PR=RB\).
Vậy P là trung điểm của AR và ta cũng có P là trung điểm AQ nên tứ giác ARQE là hình bình hành.
Bài này mình làm xong rồi nhưng lỡ tay bấm nút hủy.
MONG CÁC BẠN

a: Xét tứ giác BEFA có
BE//AF
BE=FA
BE=BA
=>BEFA là hình thoi
b: góc B=180-60=120 độ
=>góc IBE=60 độ
mà IB=BE
nên ΔIBE đều
=>góc EIB=60 độ=góc A
=>AIEF là hình thang cân
c:
Xét ΔABD có
BF là trung tuyến
BF=AD/2
Do đo: ΔABD vuông tại B
Xét tứ giác BICD có
BI//CD
BI=CD
góc IBD=90 độ
Do đó: BICD là hình chữ nhật
d: Xét ΔAED có
EF là trung tuyến
EF=AD/2
=>ΔAED vuông tại E
=>góc AED=90 độ

a: Xét tứ giác BEDF có
DE//BF
DE=BF
Do đó: BEDF là hình bình hành
b: Xét ΔAQD có
E là trung điểm của AD
EP//QD
Do đó: P là trung điểm của AQ
Suy ra;AP=PQ(1)
Xét ΔCPB có
F là trung điểm của BC
FQ//BP
Do đó: Q là trung điểm của CP
Suy ra: QC=PQ(2)
Từ (1) và (2) suy ra AP=PQ=QC





