Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 42.
Ta có:
\(\dfrac{R_1}{R_2}=\dfrac{\rho_1}{\rho_2}=2\)\(\Rightarrow\rho_2=\dfrac{\rho_1}{2}=\dfrac{2,8\cdot10^{-8}}{2}=1,4\cdot10^{-8}\left(\Omega.m\right)\)
Câu 43.
\(R_{tđ}=R_1+R_2=30+10=40\Omega\)
\(U_{max}\Leftrightarrow I_{min}\Rightarrow I=1A\)
\(\Rightarrow U_{max}=1\cdot40=40V\)

- Tính được điện trở cuả dây xoắn là:
\(R=p\frac{l}{s}=5,4.10^{-4}.\frac{10}{0,2.10^{-6}}=27\left(\Omega\right)\)
- Cường độ dòng điện qua bếp : I = \(I=\frac{U}{R}=\frac{220}{27}=8,14\left(A\right)\)
- Tính được nhiệt lượng cần cho nước đã cho đến sôi(Q hữu ích):
Q = cm(t2 – t1) = 4200 J/kg.K.2kg.(100 -15) = 714000J
- Do bếp có hiệu suất nên nhiệt lượng bếp phải cấp :
\(H=\frac{Qi}{Q}.100\%\)80% =>\(Q=\frac{Qi.100\%}{H}=\frac{71400.100\%}{80\%}=892500\left(J\right)\)
- Nhiệt lượng này do điện năng chuyển thành từ dây xoắn. Vậy thời gian cần thiết cho nước sôi :
Q = A = U.I.t = >t = \(\frac{Q}{UI}=\frac{892500}{220.8,14}=497,8\left(s\right)\) = 8,3(phút)
cái đáp án điện trở có phải sai rồi không ? Tôi bấm máy nó lại ra 27000 ohm ấy

Ta có: \(\left\{{}\begin{matrix}R_1=\rho_1\dfrac{l_1}{S_1}\\R_2=\rho_2\dfrac{l_2}{S_2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}l_1=l_2\\S_1=S_2\\R_1=2R_2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2R_2}{R_2}=\dfrac{\rho_1}{\rho_2}\)
\(\Rightarrow\rho_2=\dfrac{\rho_1}{2}=\dfrac{0,6.10^{-8}}{2}=3.10^{-9}=0,3.10^{-8}\left(\Omega m\right)\)
=> Chọn C

Bài 1.
a. Khi dòng điện đi qua ấm, điện năng đã biến thành nhiệt năng
Điện trở của dây làm ấm là: \(P=\frac{U^2}{P}=\frac{200^2}{1100}=44\Omega\)
b. Có:
\(V=1,8l\Rightarrow m=1,8kg\)
\(C=4200J/kg.K\)
\(\hept{\begin{cases}t_1=25^oC\\t_2=100^oC\end{cases}}\)
Nhiệt lượng cần thiết để đun sôi nước là: \(Q=m.C.\left(t_2-t_1\right)=1,8.4200.\left(100-25\right)=567000J\)
Thời gian để nước sôi là: \(t=\frac{Q}{P}=\frac{567000}{1100}=515,45\) giây
Bài 2.
Nhiệt lượng toả ra để đun sôi nước là: \(Q=m.c.\left(t_1-t\right)=2,5.4200.\left(100-25\right)=787500J\)
Thời gian đun nước là: \(t=\frac{Q}{P_{dm}}=\frac{787500}{900}=875s\)

a. \(R=p\dfrac{l}{S}=0,4.10^{-6}\dfrac{3}{0,3\cdot10^{-6}}=4\Omega\)
b. \(\left\{{}\begin{matrix}Q_{thu}=mc\Delta t=5.4200.80=1680000\left(J\right)\\Q_{toa}=A=UIt=220.\left(\dfrac{220}{4}\right).50.60=3630000\left(J\right)\end{matrix}\right.\)
\(\Rightarrow H=\dfrac{Q_{thu}}{Q_{toa}}100\%=\dfrac{1680000}{3630000}100\%\approx46,3\%\)

Okie iem :3
\(Q=P.t=1000.t\left(J\right)\)
\(Q_{toa}=mc\left(100-20\right)=4.4200.80\left(J\right)\)
Áp dụng phương trinh cân bằng nhiệt:
\(\Rightarrow Q=Q_{toa}\Leftrightarrow1000t=4.4200.80\Rightarrow t=...\left(s\right)\)
b/ Con số 1000 W cho biết công suất của ấm khi hoạt động bình thường
c/ Điện trở được gập làm đôi, nghĩa là cắt dây đó thành 2 phần bằng nhau rồi mắc song song
\(R'=\dfrac{1}{2}R=\dfrac{1}{2}.\dfrac{U^2_{dm}}{P_{dm}}=\dfrac{1}{2}.\dfrac{220^2}{1000}=...\left(\Omega\right)\)
\(\Rightarrow R_{td}=\dfrac{R'}{2}=...\left(\Omega\right)\Rightarrow Q'=\dfrac{U^2_{dm}}{R_{td}}.t\left(J\right)\)
\(\Rightarrow Q'=Q_{toa}\Leftrightarrow\dfrac{220^2}{R_{td}}.t'=4.4200.80\Rightarrow t'=...\left(s\right)\)
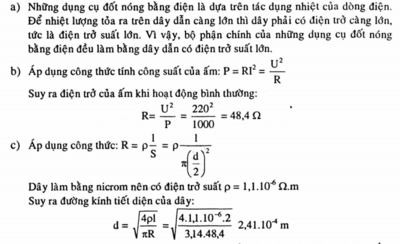
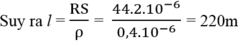
Tham khảo
a) Nhiệt lượng cần cung cấp để đun sôi lượng nước trên là:
Q1 = c.m.(T – T0) = 4200.2.(100 - 20) = 672000 (J)
b) Hiệu suất của bếp:
Nhiệt lượng mà ấm điện đã tỏa ra khi đó là:
c) Từ công thức: Qtp = A = P.t
→ Thời gian đun sôi lượng nước: