Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
b: Hình bình hành AMND có AM=AD
nên AMND là hình thoi
c: Xét tứ giác ANKQ có
D là trung điểm của NQ
D là trung điểm của AK
Do đó: ANKQ là hình bình hành

a) Xét ΔABC có
M là trung điểm của BC(gt)
F là trung điểm của AC(gt)
Do đó: MF là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: MF//AB và \(MF=\dfrac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)
mà E\(\in\)AB và \(AE=\dfrac{AB}{2}\)(E là trung điểm của AB)
nên MF//AE và MF=AE
Xét tứ giác AEMF có
MF//AE(cmt)
MF=AE(cmt)
Do đó: AEMF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Hình bình hành AEMF trở thành hình chữ nhật khi \(\widehat{BAC}=90^0\)
c) Xét tứ giác AMCK có
F là trung điểm của đường chéo AC
F là trung điểm của đường chéo MK
Do đó: AMCK là hình bình hành(Dấu hiệu nhận biết hình bình hành)

Câu a bạn sửa lại để đi mình giải cho .
Sao lại chứng minh ABCD là hình bình hành

Bài làm:
a, hbh ABCD có: AB // CD và AB = CD
=> AM // DN và AM = DN
=> AMND là hbh mà AB = 2AD => 1/2AB = AD => AM = AD
=> AMND là hthoi
b, cmtt câu a ta có: MB // ND và MB = ND
=> MBND là hbh

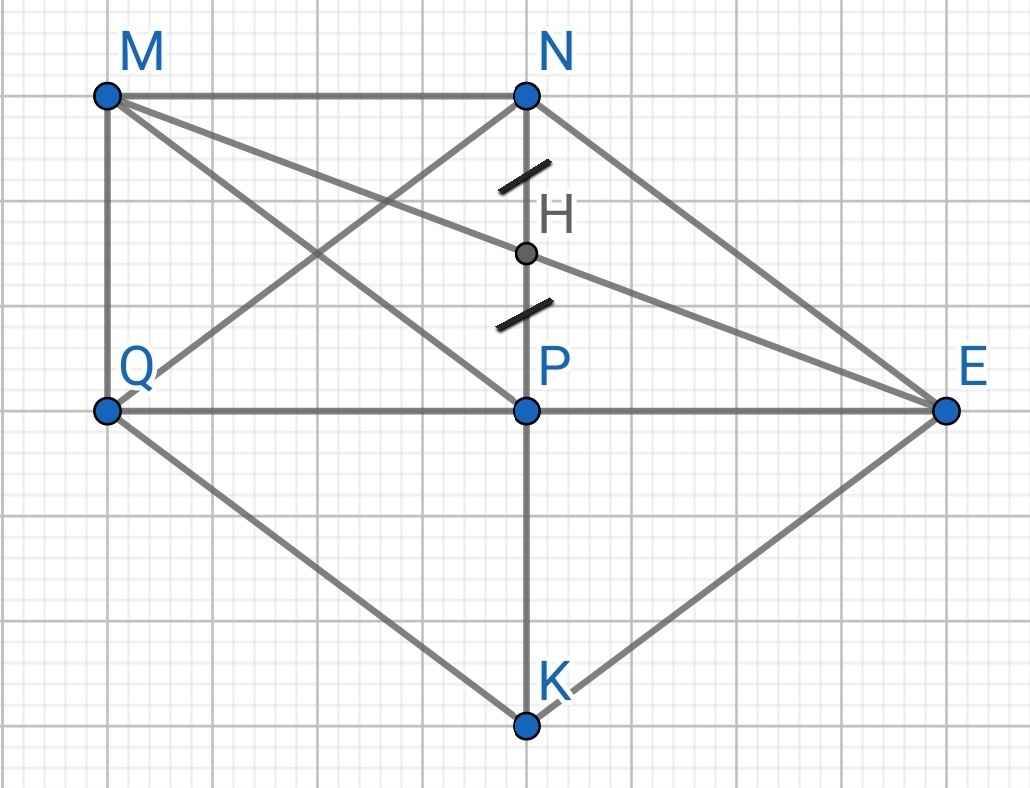 a) Do MNPQ là hình chữ nhật (gt)
a) Do MNPQ là hình chữ nhật (gt)
⇒ NP ⊥ PQ
⇒ NP ⊥ PE
Xét hai tam giác vuông: ∆NHM và ∆PHE có:
NH = HP (gt)
NHM = PHE (đối đỉnh)
⇒ ∆NHM = ∆PHE (cạnh góc vuông - góc nhọn kề)
b) Do ∆NHM = ∆PHE (cmt)
⇒ MN = PE (hai cạnh tương ứng)
Do MNPQ là hình chữ nhật (gt)
⇒ MN // PQ
⇒ MN // PE
Tứ giác MNEP có:
MN // PE (cmt)
MN = PE (cmt)
⇒ MNEP là hình bình hành
c) Do MNPQ là hình chữ nhật
⇒ MN = PQ
Mà MN = PE (cmt)
⇒ PQ = PE
⇒ P là trung điểm của QE
Do N và K đối xứng với nhau qua P (gt)
⇒ P là trung điểm của NK
Do NP ⊥ PQ (cmt)
⇒ NK ⊥ QE
Tứ giác QNEK có:
P là trung điểm của QE (cmt)
P là trung điểm của NK (cmt)
⇒ QNEK là hình bình hành
Mà NK ⊥ QE (cmt)
⇒ QNEK là hình thoi
a. Ta có:
- H là trung điểm của NP, nên NH = HM.
- E là giao điểm của MH và PQ, nên HE = EP.
- Ta cũng có NM = NP (do H là trung điểm của NP).
Vậy, ta có NHM ≅ PHE theo nguyên tắc cạnh - cạnh - cạnh.
b. Ta có:
- M là trung điểm của NE (do H là trung điểm của NP).
- H là trung điểm của NP (do H là trung điểm của NP).
Vậy, ta có MNEP là hình bình hành theo định nghĩa của hình bình hành.
c. Gọi K là điểm đối xứng của N qua P. Ta cần chứng minh tứ giác QNEK là hình thoi.
- Ta có NP = NK (do K là điểm đối xứng của N qua P).
- Ta cũng có NQ = NE (do MNEP là hình bình hành).
- Vì NP = NK và NQ = NE, nên ta có NPQ ≅ NKE theo nguyên tắc cạnh - cạnh - cạnh.
- Do đó, góc NQK = góc NEK.
- Nhưng góc NEK = góc NHE (do NHM ≅ PHE).
- Vậy, góc NQK = góc NHE.
- Ta cũng có góc QNK = góc ENH (do NHM ≅ PHE).
- Vậy, tứ giác QNEK có hai cặp góc đối nhau bằng nhau, nên QNEK là hình thoi theo định nghĩa của hình thoi.
a: Xét tứ giác MNEP có
H là trung điểm của NP
H là trung điểm của ME
Do đó: MNEP là hình bình hành
b: Ta có: MNEP là hình bình hành
=>MN//PE
mà QP//MN
và PE,QP có điểm chung là P
nên E,P,Q thẳng hàng