Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(\overrightarrow {{u_{AB}}} = \overrightarrow {AB} = \left( {100;180} \right)\) suy ra \(\overrightarrow {{n_{AB}}} = \left( {{9_1}; - 5} \right)\).
Mặt khác AB đi qua điểm \(A\left( {0;32} \right)\) nên phương trình của AB là \(9x - 5y + 160 = 0 \Leftrightarrow x = \frac{{5y - 160}}{9}\).
Với \(y = 0{{\rm{ }}^o}F\) ta có: \(x = \frac{{5.0 - 160}}{9} = \left( {\frac{{ - 160}}{9}} \right){{\rm{ }}^o}C\)
Với \(y = 100{{\rm{ }}^o}F\) ta có: \(x = \frac{{5.100 - 160}}{9} = \left( {\frac{{340}}{9}} \right){{\rm{ }}^o}C\)
Vậy \(0{{\rm{ }}^o}F\),\(100{{\rm{ }}^o}F\)tương ứng xấp xỉ \( - 18{{\rm{ }}^o}C,38{{\rm{ }}^o}C\).

a) Nhiệt độ trung bình trong năm ở Hà Nội là: \(\overline X = \frac{{16,4 + 17,0 + 20,2 + 23,7 + 27,3 + 28,8 + 28,9 + 28,2 + 27,2 + 24,6 + 21,4 + 18,2}}{{12}} = 23,5\)
b) Nhiệt độ trung bình của tháng có giá trị thấp nhất là: \(16,4\left( {^oC} \right)\)
Nhiệt độ trung bình của tháng có giá trị cao nhất là: \(28,9\left( {^oC} \right)\)

a) Bảng 6:
| Lớp nhiệt độ (ºC) | Tần suất (%) | Giá trị đại diện |
| [15; 17] | 16,7 | 16 |
| [17; 19) | 43,3 | 18 |
| [19; 21) | 36,7 | 20 |
| [21; 23] | 3,3 | 22 |
| Cộng | 100 (%) |
Số trung bình cộng của bảng 6 là:
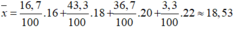
Số trung bình cộng của bảng 8 là:
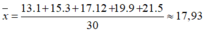
b) Nhiệt độ trung bình của thành phố Vinh trong tháng 12 cao hơn nhiệt độ trung bình trong tháng 2 khoảng 0,6ºC.

Đáp án: C
Ta có một năm có 365 ngày, một ngày có 24 giờ, một giờ có 60 phút và một phút có 60 giây.
Vậy một năm có 24.365.60.60 = 31536000 giây.
Vì vận tốc ánh sáng là 300 nghìn km/s nên trong vòng một năm nó đi được 31536000.300 = 9,4608.109 km.
0 km vì 1 vật có khối lượng ko thể đạt tới vận tốc ánh sáng, và chắc chắc ko có nhà khoa học nào lại nghiên cứu 1 máy bay vs tốc độ 7 lần vận tốc ánh sáng

Phương trình đường thẳng d: y = kx − 3
Phương trình hoành độ giao điểm của (P) và d : - x 2 + 4 x - 3 = k x - 3
⇔ - x 2 + 4 - k x = 0 ⇔ x - x + 4 - k = 0 1
d cắt đồ thị (P) tại 2 điểm phân biệt khi (1) có 2 nghiệm phân biệt ⇔ 4 - k ≠ 0 ⇔ k ≠ 4
Ta có E x 1 ; k x 1 − 3 , F x 2 ; k x 2 − 3 với x 1 , x 2 là nghiệm phương trình (1)
Δ O E F vuông tại O ⇒ O E → . O F → = 0 ⇔ x 1 . x 2 + k x 1 − 3 k x 2 − 3 = 0
⇔ x 1 . x 2 1 + k 2 − 3 k x 1 + x 2 + 9 = 0 ⇔ 0. 1 + k 2 − 3 k ( 4 − k ) + 9 = 0
⇔ k 2 − 4 k + 3 = 0 ⇔ k = 1 k = 3
Đáp án cần chọn là: D

Tham khảo:
a) Tập xác định \(D = \{ - 2; - 1;0;1;2;3;4\} \)
b) Đồ thị gồm 7 điểm A (-2; 8), B (-1; 3), O (0; 0), D (1; -1), E (2; 0), G (3; 3), H (4; 8) như hình dưới
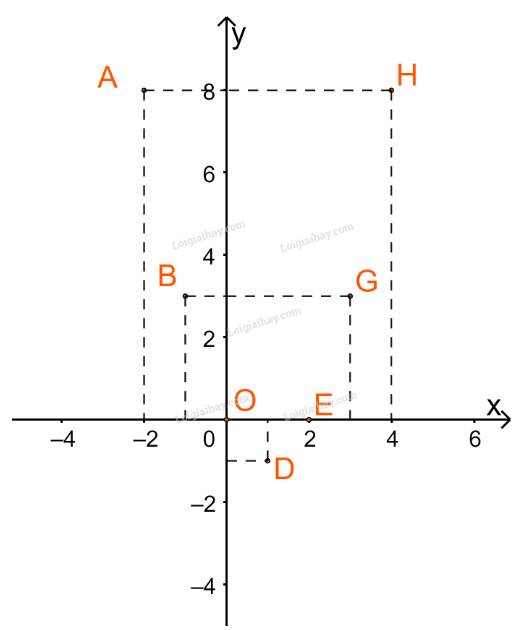

Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D


\(t\left(d\right)=-0,0018d^2+0,657d+50,95\)
=\(-0,0018\left(d^2-365d+33306,25\right)+110,90125\)
= \(-0,0018\left(d-\dfrac{365}{2}\right)^2+110,90125\le110,90125\)
\(t\left(d\right)=110,90125\Leftrightarrow d-\dfrac{365}{2}=0\Leftrightarrow d=\dfrac{365}{2}\)
Vậy nhiệt độ cao nhất rơi vào ngày thứ 182 hoặc 183 kể từ 1/1/2003